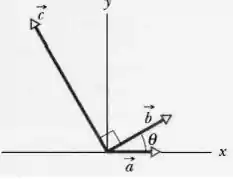
Os três vetores na Figura abaixo têm módulos a = 3; 00 m, b = 4; 00 m, c = 10; 0 m e o ângulo =. Quais são
(a) a componente x e
(b) a componente y de ;
(c) a componente x e
(d) a componente y de ; e
(e) a componente x e
(f) a componente y de ?
Se , quais são os valores de
(g) p e
(h) q?
Passo 1
O problema deu um gráfico com três vetores, deu também os módulos dos vetores e o ângulo que faz com a horizontal. Então a ideia é casar os dados com o desenho para determinar as componentes. Mas calma, vou fazer com você!
Letra (a) e (b):
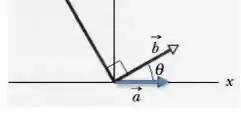
então a componente x de :
E a componente de y:
Assim o vetor é:
Passo 2
Letras (c) e (d): o vetor tem módulo e faz um ângulo com a horizontal. Então esse vetor pode ser descrito por suas componentes vertical e horizontal com ajuda do módulo (em vermelho) e das funções seno e cosseno:
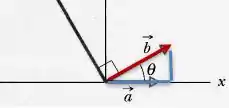 a componente x (horizontal) é o cateto adjacente desse triângulo:
a componente x (horizontal) é o cateto adjacente desse triângulo:
E a componente y (vertical) é o cateto oposto a :
Assim o vetor em termos dos vetores que dão a direção e sentido positivos dos eixos x e y é:
Notem que esse vetor tem suas componentes positivas.
Certo? Vamos olhar agora para o vetor ?
Passo 3
Agora as letras (e) e (f): vamos olhar para o vetor :
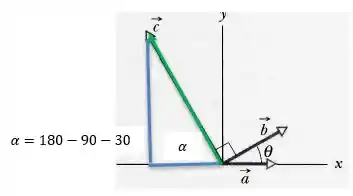
Por simetria, o ângulo que o vetor em verde faz com o lado negativo de x é Notem que agora a componente x do vetor vai ser negativa! A componente y segue sendo positiva. Então usando seno e cosseno, podemos achar as componentes, sabendo que o módulo do vetor (será nossa hipotenusa) é :
Assim o vetor em termos dos vetores que dão a direção e sentido positivos dos eixos x e y é:
Passo 4
Letras (g) e (h): Agora o problema nos diz que o vetor vai ser escrito em termos dos outros dois vetores, da seguinte forma:
Bom, sabemos que um vetor só é igual ao outro quando suas componentes são todas iguais. Então é essa propriedade que vou usar aqui: as componentes de devem ser iguais às de (multiplicado por uma constante p) e de (multiplicado por q):
Daqui temos duas equações para achar as constantes que satisfazem essa igualdade:
Da segunda temos o valor de :
E substituindo na primeira:
Assim os valores de e são:
E é isso!
Espero ter ajudado!