Sejam e dois vetores e o vetor resultante da soma entre eles. Então, podemos afirmar que:
(a) o módulo de é sempre menor que a soma dos módulos de e .
(b) o módulo de é sempre maior que a soma dos módulos de e .
(c) o módulo de nunca é igual à soma dos módulos de e .
(d) o módulo de pode ser nulo mesmo quando e são não nulos.
(e) o módulo de só é nulo quando e são nulos.
Passo 1
Pela desigualdade triangular aplicada aos módulos dos vetores:
Passo 2
Pela desigualdade observamos que as alternativas (a), (b) e (c) são incorretas.
Suponhamos agora a seguinte configuração, com os vetores e possuem mesma direção mas sentidos opostos:
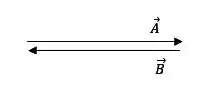
O vetor é um vetor nulo, apesar dos vetores que o compõem serem não-nulos. Desta forma, a alternativa (d) está correta e a alternativa (e) incorreta.
Resposta
(d)