Ouvindo o ruído de uma serpente, você faz dois deslocamentos rápidos de e . Usando diagramas (aproximadamente em escala), mostre como esses deslocamentos deveriam ser efetuados para que a resultante tivesse módulo igual a:
Passo 1
Para definir como esses deslocamentos são feitos, vamos usar o ângulo entre os dois vetores e (assumindo que um começa onde o outro termina).
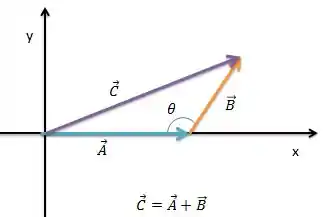
Passo 2
Alternativa a)
Assim:
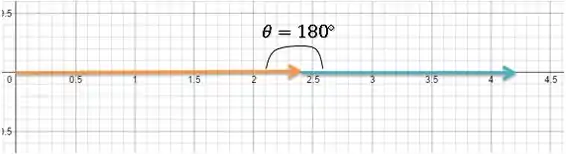
Passo 3
Alternativa b)
Assim:
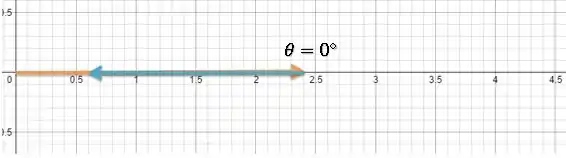
Passo 4
Alternativa c)
Bom, repara que temos dois ângulos possíveis para .
Tanto o ângulo quanto o ângulo têm cosseno igual a zero:
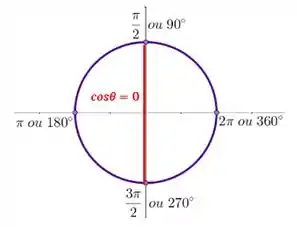
Mas como o enunciado não especifica exatamente a direção dos deslocamentos, dando apenas uma condição de deslocamento resultante, vamos escolher o menor dos ângulos:
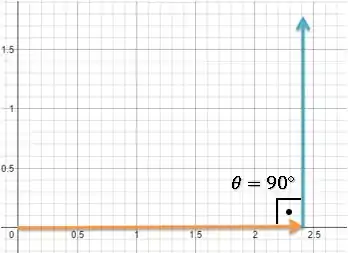
Porém, repara que os ângulos somam (uma volta completa). Portanto, ao escolhermos um dos ângulos, o outro vai aparecer da mesma maneira:
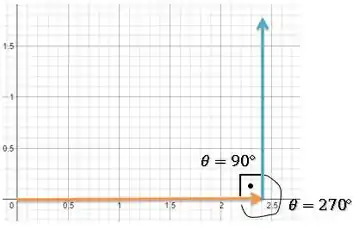
Resposta
a)
b)
c)