Considere o lançamento de projéteis num plano , onde o vetor aceleração pode ser escrito assim: Sobre o movimento do projétil, marque a alternativa incorreta:
(a) A velocidade do projétil ao longo da direção é constante;
(b) A aceleração do projétil ao longo da direção é zero;
(c) A velocidade do projétil ao longo da direção é constante;
(d) A aceleração do projétil ao longo da direção é ;
(e) A trajetória do projétil será uma parábola do tipo , onde , e são constantes.
Passo 1
Vamos analisar cada uma dessas afirmativas e achar qual delas é a incorreta.
(a) A velocidade do projétil ao longo da direção é constante;
A aceleração é a variação da velocidade. Ou seja, se a aceleração em é nula, a velocidade não vai variar nessa direção ao longo do movimento.
A afirmativa (a) está correta.
Passo 2
(b) A aceleração do projétil ao longo da direção é zero;
A aceleração em é nula pois sua componente de aceleração do vetor unitário é zero.
Inclusive já consideramos isso na alternativa passada. Caso a letra (b) estivesse incorreta, a letra (a) também estaria.
A afirmativa (b) está correta.
Passo 3
(c) A velocidade do projétil ao longo da direção é constante;
(d) A aceleração do projétil ao longo da direção é ;
Olhando para a expressão da aceleração:
Vemos que a aceleração da componente é , portanto essa será sua aceleração na direção do eixo .
Logo a afirmativa (d) está correta.
Já que existe uma aceleração na direção do eixo , sua velocidade vai variar, portanto não pode ser constante.
Achamos que a afirmativa (c) é a incorreta.
Passo 4
(e) A trajetória do projétil será uma parábola do tipo , onde , e são constantes.
Se pensarmos no eixo na vetical , sendo a aceleração a da gravidade apontando para baixo, e o eixo na horizontal, fica um pouco mais fácil de visualizar o movimento.
Se a velocidade em é constante, o projétil vai realizar um movimento uniforme na horizontal e um movimento uniformemente variado na vertical. Ou seja, uma trajetória parabólica.
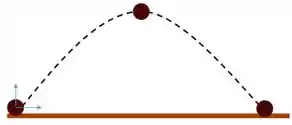
Se ainda não tem certeza disso, você pode tentar escrever os movimentos em cada eixo.
No eixo , temos um movimento com a aceleração constante:
Já no eixo , temos um movimento com velocidade constante:
Ambos está em função do tempo, então vamos isolar e tentar escrever a posição de em função da posição em :
Substituindo em , temos:
Todos os termos entre parêntesis são constantes, então podemos escrever como:

Claramente, você não precisa fazer isso na prova kkk. Só o fato de um eixo ter aceleração nula e o outro ter uma aceleração constante, faz do movimento uma parábola e pode ser escrita daquela maneira.
A afirmativa (e) está correta.
Resposta
Letra (c)