3. Sobre a função da Questão 2, quantas soluções possui a equação ?
Passo 1
Oi, galerinha! Tudo bom? Olhando para a Questão 2, nós temos o seguinte gráfico da função,
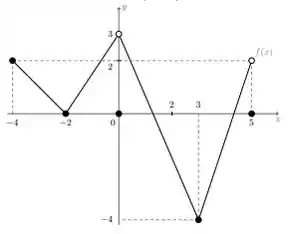
E queremos saber quantas soluções são possíveis . Para isso temos que ver primeiro para quais temos que e depois ver para quais temos que .
Bora lá!
Passo 2
Olhando para o gráfico para descobrir quais valores de dão .
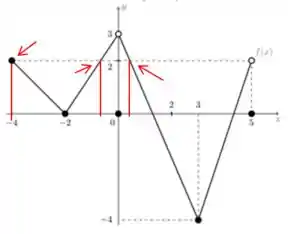
Repara que temos pontos! Agora temos que verificar quais soluções existem para encontrarmos cada um desses pontos.
Agora esses 3 valores de x serão os valores da função. Pra cada um deles, vamos achar os valores de x (ou pelo menos quantos x existem).
Passo 3
Para , temos que apenas é possivel.
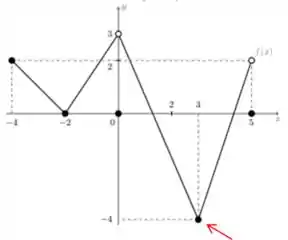
Para as outros duas setas, não temos um valor conhecido ainda. Então vamos olhar caso a caso!
Passo 4
O segundo ponto encontrado no passo 2 é um número entre e .
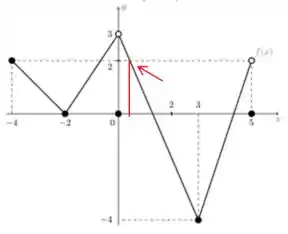
Então vamos olhar quantas vezes temos entre e .
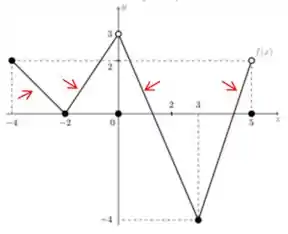
Repara que essa passa por esse ponto quatro vezes. Então temos mais soluções possíveis.
Passo 5
O terceiro ponto encontrado no passo 2 é um número entre e .
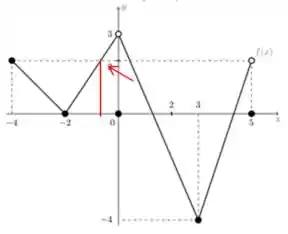
Então vamos olhar quantas vezes temos entre e .
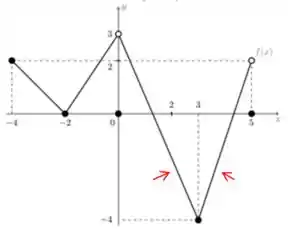
Repara que essa passa por esse ponto duas vezes. Então temos mais soluções possíveis.
Passo 6
Somando todas as soluções possíveis ficamos com
A resposta correta é a letra E.