Sobre três conjuntos A, B e C, sabe-se que , , , , , . Nestas condições, determinar:
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
Vamos desenhar um diagrama de Venn Euler aqui porque é tanta informação que se formos fazer de cabeça a gente pode se perder. Então qual é o macete nesse rolê aqui: vamos começar desenhando os valores das intersecções dos três conjuntos!!!
Depois pra conseguirmos o valor da intersecção entre DOIS conjuntos, a gente vai pegar o valor dado no enunciado e diminuir do valor da intersecção dos 3, certo?
CALMA E VEM COMIGO!
Passo 2
Vamos primeiro desenhar as intersecções.
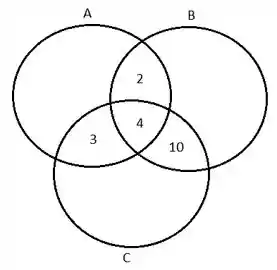
Como eu fiz esse desenho? Bem, primeiro começamos com o valor da intersecção dos 3 conjuntos que são 4 elementos, certo? Depois pra calcular quanto tinha em cada intersecção de dois conjuntos eu simplesmente peguei o valor dado no enunciado e subtrai de 4 que é a intersecção dos 3 conjuntos.
Então por exemplo, pra saber quantos estão ali na intersecção de A e C, eu fiz:
Passo 3
Agora vamos ver quanto tem de elementos exclusivos em cada conjunto. Para isso vamos pegar o valor de elementos dados no enunciado e subtrair da soma dos números das intersecções que esse conjunto tem.
No enunciado nos diz que o conjunto A tem 15 elementos, porém, 9 deles fazem parte de intersecções, logo, temos exclusivamente:
O enunciado também nos disse que:
O enunciado nos diz que:
Portanto,
Mas sabemos que desses 19 em B, 16 estão na intersecção, portanto, exclusivamente em B temos
Fazendo agora analogamente pra C, temos do enunciado que:
Porém, temos 17 fazendo parte da intersecção, logo
Ao final, nosso diagrama fica: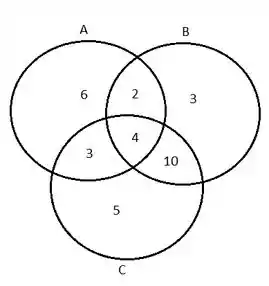
Passo 4
Agora podemos concluir as questões do enunciado:
- 𝑛𝐶−𝐴=5
Para a letra (d) queremos quantos elementos exclusivamente temos em A
Na letra (e), queremos os valores exclusivos de C
Por fim, queremos exclusivamente os valores da união de A e B
Arrasamos e agora vamos pra próxima!!

Resposta
- 𝑛𝐶−𝐴=5