UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.4c
Verificar quais dos seguintes conjuntos são conexos
Passo 1
E aí galerinha, tranquilo?
Então, nessa questão recebemos o seguinte conjunto:
Ou seja, é um conjunto cujos pontos são definidos pela equação:
Precisamos verificar se esse conjunto é conexo.
Um conjunto conexo é aquele que não pode ser separado em dois conjuntos abertos disjuntos, ou seja, que não tem intersecção. Isso significa que o conjunto não pode ser separado em pedações desconectados.
Pra verificarmos isso, tem um bizu muito legal. Vamos desenhar a região no espaço e verificar se para quaisquer dois pontos escolhidos conseguimos traçar um caminho entre eles que esteja todo contido dentro da região. Se isso acontecer, o conjunto é conexo, beleza?
Vamo nessa!
Passo 2
Bom, temos a seguinte equação definindo o conjunto:
Daí, temos:
Essa é a equação da região interna e da superfície de um elipsoide. Podemos esboçá-lo da seguinte forma:
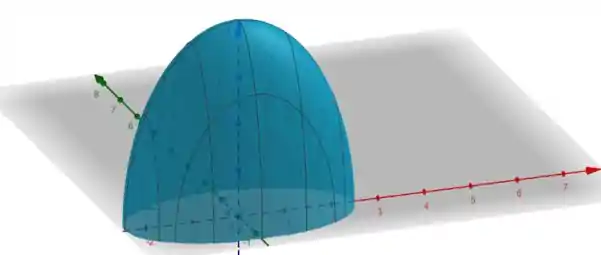
Onde a figura é simétrica com relação ao plano cinza, fechando assim o elipsoide.
Passo 3
Como vimos, o conjunto nada mais é do que um elipsoide. Assim, a gente pode perceber que ele não possui pedações desconectados. De fato, se tomarmos quaisquer dois pontos na superfície ou na região interna do elipsoide, temos um caminho dentro dele que liga os pontos.
Portanto, dizemos que o conjunto é conexo.
Obrigado pela atenção gente, até a próxima 😊
Resposta
Conexo.