Q - Um bloco de massa é colocado sobre um bloco de massa , que encontra-se em repouso. Admitindo que os coeficientes de atrito estático e cinético entre os blocos são e , respectivamente, e que os coeficientes de atrito estático e cinético entre o bloco de massa e o solo são e , respectivamente, o
máximo valor de , em Newtons, que pode ser aplicada ao corpo de massa para que o sistema permaneça em repouso é:
Passo 1
Vem comigo que a gente vai detonar essa questão juntos!
Para podermos ver melhor o que está acontecendo, vamos montar um diagrama de corpo livre, temos o seguinte então:
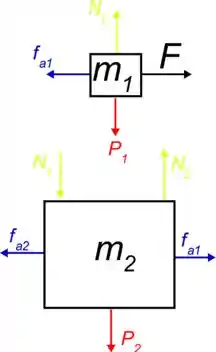
Onde as forças e são as forças normal e de atrito entre os blocos e as forças e são as forças da interação do bloco e o chão.
Como os blocos estão em repouso na direção , temos o seguinte:
Para o bloco :
Para o bloco :
Para que o sistema em repouso a força resultante em e em deve ser zero.
Vamos então aplicar a segunda lei de Newton em cada bloco e vê o que encontramos em relação a .
Passo 2
Vamos começar com o bloco , temos:
Para o bloco temos que:
Juntando as duas equações temos que:
Passo 3
Como o enunciado pede a força máxima que pode ser aplicada para que os blocos fiquem em repouso, teremos que a força máxima deve ser igual a força de atrito estático máximo, assim:
A força de atrito máxima do bloco com o chão é dada por:
Usando que:
Assim temos que:
Substituindo os valores que conhecemos, temos:
Logo temos que:
Com isso temos que:
Prontinho, encontramos o que o enunciado pedia!