Uma força horizontal empurra um bloco de massa contra uma parede vertical. O coeficiente de atrito entre o bloco e a parede é . Qual é o módulo mínimo da força que é necessário para manter o bloco sem escorregar para baixo no muro?
Passo 1
Bom galera, a relação das forças que agem no bloco pode ser vista abaixo:
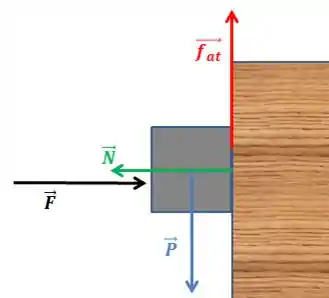
Passo 2
Como o bloco se mantêm em repouso, a soma das forças horizontais é zero e das verticas também.
Então:
Horizontais:
Verticais:
Passo 3
Então temos:
Mas, como a força de atrito pode ser calculada por:
Então:
Então:
c)
Resposta
c)