Considere o sistema da figura ao lado. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco de massa M e a superfície do piso é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa m parado sobre o de baixo, se o de baixo estiver parado. Uma força F é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma, que o bloco de cima não deslize sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força F é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a DESCER sobre o de baixo). Dê suas respostas em termos de .
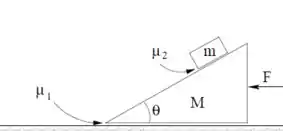
P2.4 – Determine o valor mínimo da força .
Passo 1
Faaaala meu povoo! Tudo certinho com vocês?? Bora lá resolver mais um probleminha!
Nesse item é pedido para calcular o valor mínimo da força do nosso conjunto, então vem comigo!
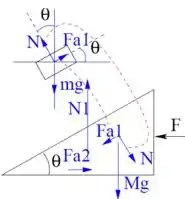
Para calcular o valor da força , no caso de o sistema ter a aceleração:
(item 2.3 da nossa questão), temos que analisar o corpo de massa . Como acontece com o corpo de massa , não há aceleração na direção vertical para . Considerando positivo para cima:
Lembrando que e usado o valor de (item 2.2 da nossa questão) dado por:
Assim, temos:
Como seria de se esperar, a normal sustenta o peso dos dois blocos. Na horizontal, por sua vez, temos, considerando positivo para a esquerda, sendo:
Ou,
Agora temos o seguinte meus jovens, o valor de , onde o já foi calculado anteriormente, sendo:
Se liga que também já temos o valor de que foi calculado no item 2.3 da nossa questão e vale:
Finalmente, substituindo esses valores na equação:, teremos:
Que simplificando, temos:
E tá aí nossa a nossa força , te ajudei?? Então te vejo na próxima!
