Um carro trafega sobre uma estrada horizontal, na forma de um círculo de raio igual a . Sabendo que o coeficiente de atrito estático é , com que velocidade o carro pode trafegar sem risco de derrapar? SE a curva não for horizontal, mas inclinada, achar o ângulo de inclinação para que o carro a possa fazer a curva na ausência de atrito no pavimento.
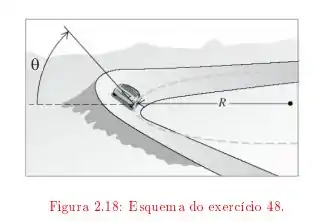
Passo 1
Oiiie, tudo bem?
Temos aqui um problema clássico que utiliza os conceitos de movimento circular! Temos duas situações, a qual temos um carro em uma pista circular sem inclinação, ao fazer a curva é possível que a velocidade faça com que ele escape da pista devido a uma força centrípeta, ou seja, o que mantém na pista é a força de atrito apontando para o centro, o sistema pode ser representado como
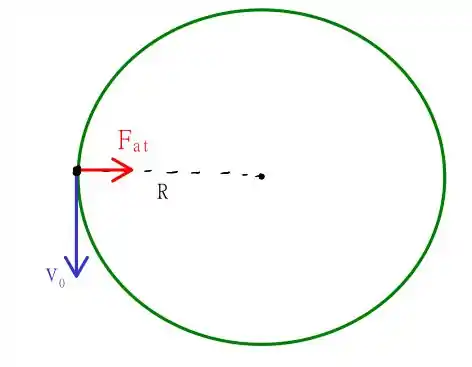
Aqui temos que o coeficiente de atrito é , o raio é , com essas informações precisamos encontrar a velocidade máxima que o carro pode entrar na curva sem derrapar! Vamos precisar lembrar alguns conceitos relacionados a intensidade da força de atrito estática, e a relação para a força centrípeta
No entanto, quando inclinamos a pista, a necessidade atrito pode desaparecer, o seguinte diagrama representa a situação
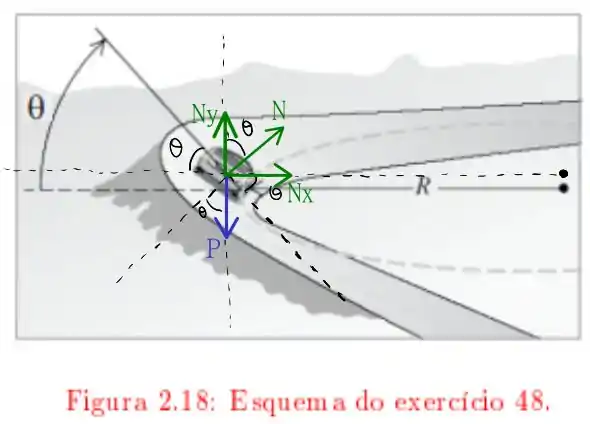
Temos que para o carro não escapar para fora da curva é necessário que o ângulo seja tal que a componente da força normal seja agora a força centrípeta no caso em que a velocidade é . Maravilha! Vamos tentar fazer isso!
Passo 2
No primeiro caso, temos que a força de atrito estático deve ser igual a força centrípeta do movimento circular, ou seja, temos que
como queremos a máxima velocidade, também iremos considerar o valor máximo da força de atrito estática, ou seja, temos que
A força normal é exatamente igual ao peso do carro, já que não há movimento vertical, sendo assim, temos que
A velocidade será então tal que
Ou seja, a velocidade será tal que
Vamos analisar agora o caso da pista inclinada!
Passo 3
Neste caso precisamos que
Usando o esquema apresentado na figura do passo , temos que
e, notando que
Portanto, obtemos
O ângulo desejado será
a velocidade é tal que , portanto, obtemos o ângulo como
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e