Bagagens são transportadas de um local a outro de um aeroporto por uma esteira . Em um certo local a esteira tem uma inclinação de com a horizontal. Suponha que para o ângulo tão pequeno as malas não escorreguem. Determine o módulo da força de atrito exercida pela esteira sobre uma caixa de de peso quando a caixa está na parte inclinada da esteira e a velocidade da esteira é (a) nula e constante, (b) e constante, (c) e aumentando a uma taxa de e (d) e diminuindo a uma taxa de e (e) e aumentando a uma taxa de . (f) Para quais dessas cinco situações a força de atrito é dirigida para baixo ao longo da rampa?
Considere que quando a mala sobe a sua velocidade é positiva.
Passo 1
Antes de começarmos, temos que entender o porque das esteiras conseguirem arrastar os corpos.
A situação a se comparar nesse caso é aquela que temos um bloco em cima do outro e existe uma força aplicada somente no bloco de baixo. Nesse caso, o bloco de cima só se move se houver atrito na superfície entre os dois blocos.
O que temos que fazer aqui é o de sempre: fazer o diagrama de corpo livre e aplicar a segunda lei de Newton. O importante a se perceber aqui é que como as malas não escorregam, a aceleração delas é igual à aceleração da esteira.
Passo 2
Vamos fazer o diagrama de corpo livre da situação da letra (a):
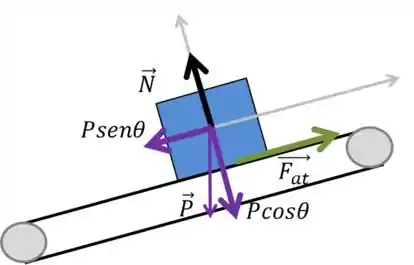
A velocidade da esteira é nula e constante, portanto, a aceleração da esteira e do bloco são nulas. Vamos portanto aplicar a segunda lei de Newton no eixo que está na direção da esteira.
Substituindo os valores de e :
Passo 3
Já para a situação da letra (b), temos que a velocidade da esteira é constante, portanto, a aceleração da esteira e do bloco são nulas. Vamos portanto aplicar a segunda lei de Newton no eixo que está na direção da esteira.
Substituindo os valores de e :
Passo 4
Na situação da letra (c), temos uma aceleração de . Considerando o eixo que colocamos na figura acima, temos então que:
Não sabemos o sentido da , mas vamos manter o diagrama com ela pra cima e, se ela der negativa, nossa suposição está errada.
Aplicando a segunda lei de Newton no sentido da esteira:
Substituindo os valores de e :
Passo 5
Na letra (d), a aceleração tem o mesmo módulo que a letra (c), mas está no sentido oposto, portanto . Aplicando a segunda lei de Newton:
Substituindo os valores de e :
Como a deu positivo, nossa suposição estava certa e ela está apontando para cima.
Passo 6
Finalmente, para a letra (e), temos a mesma coisa da letra (c), mas com um valor diferente para a aceleração que é , também para cima. Observando o sinal de menos na aceleração e aplicando a segunda lei de Newton:
Substituindo os valores de e :
Passo 7
Em nenhuma das situações a aponta para baixo.
Resposta
- Nenhuma das situações