Dois objetos e estão presos por cordas a um anel de massa desprezível. O anel também está preso a uma parede por uma terceira corda, que forma um ângulo com a horizontal. Considere que tem massa , e possui coeficientes de atrito estático e dinâmico com a mesa dados por e , respectivamente. Suponha que todas as cordas estão totalmente esticadas.
Dados: . e .
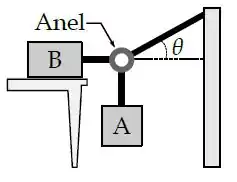
(a) Considerando que o sistema é estático (não se move), faça um diagrama indicando todas as forças que atuam sobre o anel e os objetos e .
(b) Qual o valor da massa para o qual o bloco se encontra na iminência de movimento?
(c) Suponha que . Qual o módulo da tração na corda que conecta o anel a parede?
Passo 1
Nessa questão, temos que o anel está preso aos dois blocos e à parede.
Porque esse negócio não cai?
Ah, é porque existe uma força de atrito alí entre o bloco e a superficie que ele está apoiado agindo contra o movimento.
Vamos analisar melhor isso em cada alternativa.
Passo 2
(a) Considerando que o sistema é estático (não se move), faça um diagrama indicando todas as forças que atuam sobre o anel e os objetos e .
Vamos analisar separadamente o anel e cada um dos blocos.
Começando pelo mais fácil, o bloco vai ter apenas a força peso para baixo e uma força de tração para cima impedindo que ele caia:
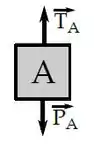
Agora, dá uma olhada no bloco .
Para compensar a força peso , vai existir uma força normal para cima. Além disso, a corda tem uma força de tração que puxa o bloco para a direita, logo, vai existir uma força de atrito contrária à tendência de deslizamento, ou seja, para a esquerda:
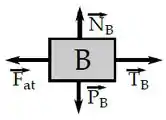
Por último, vamos ao anel.
O diagrama do anel é bem fácil, cada corda ligada a ele vai exercer uma força de tração:
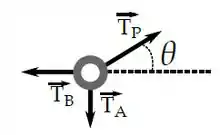
Passo 3
(b) Qual o valor da massa para o qual o bloco se encontra na iminência de movimento?
Olha aqui o que está acontecendo:
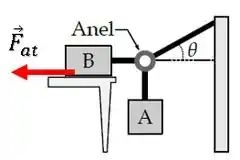
Você concorda comigo que a única força resistindo ao movimento do sistema é essa força de atrito no bloco ?
Sim, né. Além disso, a gente sabe que a força de atrito estático tem um valor máximo igual a:
Então,se a gente for aumentando a massa do bloco , a força com que a corda puxa o bloco vai aumentando também. Isso acontece até um dado momento que ela ultrapassa a e o sistema se move.
Esse instante limite antes do bloco se mover é chamado de iminência do movimento.
Então, vamos descobrir qual a massa do bloco que faz a força de atrito no bloco ser máxima.
Passo 4
Olhando para o diagrama do bloco , temos que:
Agora, vamos fazer o somatório das forças no anel.
Podemos decompor a força de tração da parede da seguinte maneira:
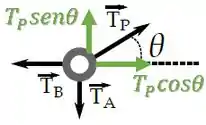
Pelo equilíbrio na vertical temos que:
Se , então:
Já com o somatório de forças na horizontal , temos que:
Dividindo a equação pela equação , chegamos em:
Ou seja, a tração que atua no bloco será:
Passo 5
Agora, basta fazer o somatório de forças em e matar a questão.
Voltando aqui o diagrama do bloco .
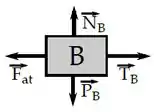
Pelo equilíbrio vertical, temos que:
Já pelo equilíbrio horizontal, temos que:
Bom, já achamos que , então:
Se queremos a , a nossa expressão fica assim:
Calma, falta muito pouco.

Achamos no equilíbrio vertical que . Além disso, a força peso é , então:
Assim, a massa do bloco é igual a:
Já podemos substituir e correr pro abraço, lembrando que a :
Passo 6
(c) Suponha que . Qual o módulo da tração na corda que conecta o anel a parede?
Agora que temos a massa do bloco , conseguimos calcular a força de tração com a parede a partir da relação que já fizemos para o anel:
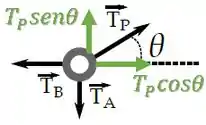
Lembrando que ...
Assim, basta substituir os valores que temos e achar :
Resposta
(a)
Bloco :
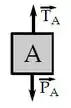
Bloco :
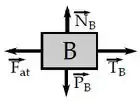
Anel:
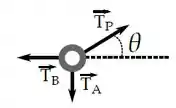
(b)
(c)