Um bloco de está sobre outro de que repousa sobre uma mesa lisa (sem atrito). Os coeficientes de atrito estático e cinético entre os blocos são 0,4 e 0,3, respectivamente. Uma força é aplicada ao bloco de paralelamente à superfície da mesa (veja a figura).
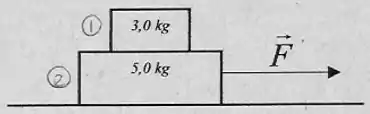
a) Faça um diagrama de forças para cada um dos blocos.
b) Qual é o valor máximo do módulo de que não provoca o escorregamento do bloco de sobre o de ?
c) Calcule a aceleração de cada bloco se for igual a .
Passo 1
a)
Os blocos sofrem ação das forças peso e normal. Além disso, tem também ação dos pares ação e reação, que nesse caso é a força de atrito e a força de contato entre os blocos .
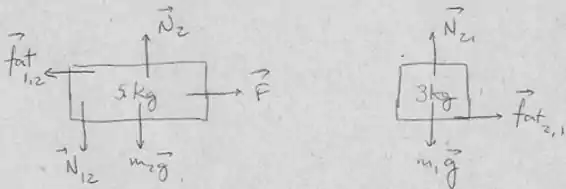
Passo 2
b)
Como não há escorregamento, entrará em ação então a força de atrito estática, onde segundo o enunciado, .
Aplicando a segunda lei de Newton no eixo :
Bloco 1:
Utilizando a fórmula da força de atrito:
Agora, aplicando a segunda lei de Newton no sistema como um todo, temos:
Substituindo a aceleração que encontramos:
Entretanto, sabemos que .
Passo 3
c)
Isso quer dizer que se a força ultrapassou a força máxima, então haverá o escorregamento, e o enunciado nos deu que .
Aplicando a segunda lei de Newton:
Bloco 2:
Lembrando que
Substituindo:
Bloco 1:
Resposta
a)
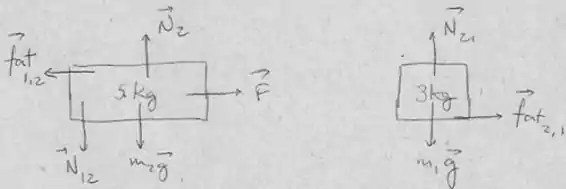
b)
c)