Marque a alternativa que indica a transformada inversa da função
( )
( )
( )
( )
( )
Passo 1
Opa, vamos lá. A questão quer que a gente calcule a transformada inversa da nossa função:
Bom, podemos começar fazendo frações parciais pra nos ajudar. Então a gente separa o denominador e coloca as constantes e no numerador para poder descobrir o valor delas:
Agora podemos fazer a igualdadedo numerador e descobrir os valores das constantes;
Podemos isolar na primeira equação e substituir na segunda.
Agora que sabemos , podemos voltar na equação para acharmos .
Maravilha! Descobrimos os valores das constantes. Agora podemos substituir na nossa fomra de frações parciais:
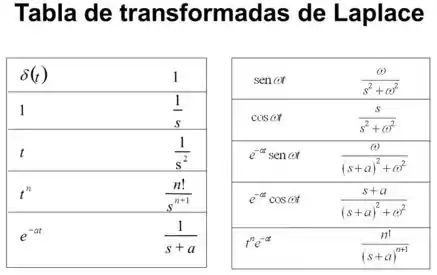
Com as frações parciais, a gente precisa olhar aquela tabela de transformadas de Laplace pra descobrirmos qual é a inversa. Coloquei uma tabela aqui, dá ma olhadinha.
A nossa função tem uma estrutura bem parecida com a da exponencial, não é? Nossa inversa então, fica: