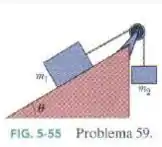
Um bloco de massa sobre um plano sem atrito inclinado, de ângulo , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um outro bloco de massa (Fig 5-55). Quais são (a) o módulo da aceleração de cada bloco, (b) a orientação da aceleração do bloco que está pendurado e (c) a tensão da corda?
Passo 1
Temos aqui um problema de análise de corpos sobre forças, onde são pedidas as acelerações dos blocos e a tensão que age sobre os dois blocos. Aprendemos que, fazendo os Diagramas de corpo livre e aplicando a segunda lei de Newton, conseguimos esses resultados. No entanto, a única jogada desse problema que é necessária para resolvê-lo fora isso é usando que a corda é inextensível, e portanto, como os deslocamentos são iguais, O MÓDULO das acelerações são iguais.
Isso mesmo! É importante ressaltar que apenas o módulo das acelerações são iguais, já que, as direções que os blocos se movimentam são diferentes.
Passo 2
Com as considerações do passo anterior, podemos começar a fazer o diagrama de corpo livre dos dois blocos, lembrando também que a tensão é a mesma ao longo do fio.
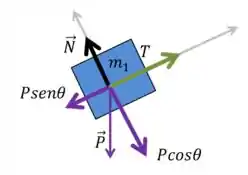
Como este corpo não entra no plano e nem sai dele, concluímos que a aceleração dele está na direção do plano inclinado, portanto, aplicando a segunda lei de Newton no eixo do movimento, temos:
Perceba que foi admitido que é positivo, ou seja, está na direção do eixo indicada na figura, subindo o plano inclinado. Caso nossa suposição esteja errada, dará um resultado negativo.
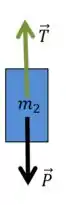
Percebe-se que este corpo também está fadado a se movimentar somente no sentido vertical, já que não existem forças horizontais atuando nele (o que já responde parcialmente a letra (b)). Além disso, devemos ficar ligados com as direções que chutamos, para que não haja discordância. No corpo de massa , supomos que ele está subindo o plano, portanto, necessariamente temos que admitir que este bloco, de massa , está descendo.
Aplicando então a segunda lei de Newton:
Se somarmos as duas equações obtidas, temos que:
Concluímos anteriormente que:
Aplicando este resultado e substituindo os valores conhecidos:
Passo 3
Para concluir a resposta da letra (b), precisamos saber o sentido do movimento do bloco pendurado. Como a resposta de deu positiva, nossas suposições estavam certas e o bloco pendurado está descendo.
Portanto, o bloco pendurado está se movendo verticalmente para baixo com aceleração .
Passo 4
Sabendo a aceleração dos corpos, podemos coloca-la em qualquer equação encontrada anteriormente para descobrirmos a tensão no fio. Vamos escolher a :
E então:
Resposta
- Verticalmente para baixo