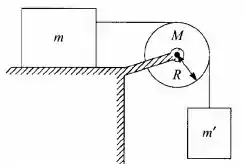
Na figura ao lado um bloco de massa desliza sobre um plano horizontal com coeficiente de atrito cinético . Ele está ligado por uma corda ideal, que passa por uma polia (disco uniforme de raio e massa ), a um outro bloco de massa que está suspenso. Considere que a corda não escorrega na polia, e que não há atrito no eixo da polia. O sistema é solto do repouso em e as massas entram em movimento.
b) Qual a velocidade linear dos blocos e a velocidade angular da polia após o bloco descer uma altura ? A velocidade angular é positiva ou negativa nesse caso?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um exemplo clássico de Lei de Newton envolvendo dois blocos envolvendo várias forças.
A questão nos pede para descobrirmos a velocidade linear dos blocos e a velocidade angular da polia após o bloco descer uma altura .
Também, nos pergunta se a aceleração angular é positiva ou negativa nesse caso.
Uma dica é analisarmos os diagramas de corpo livre de cada bloco e aplicar a Lei de Newton!
E aí? Bora lá?
Passo 2
Bom... pela equação de Torricelli, podemos encontrar a velocidade linear dos blocos :
Pela letra a), descobrimos que a aceleração é dada por:
Assim, substituindo, temos:
Passo 3
Para a velocidade angular da polia, temos:
Pela equação de Torricelli para o movimento angular, temos de modo análogo ao Passo 2:
Substituindo pelo valor que encontramos na letra a), temos:
Como a velocidade angular realiza o movimento no sentido horário, ela é dita como negativa.
Entendeu direitinho? Responde aee ;)

Resposta
Como a velocidade angular realiza o movimento no sentido horário, ela é dita como negativa.