Três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas são , e . Quando o conjunto é liberado a partir do repouso.
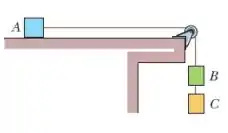
que distância percorre nos primeiros (supondo que não atinja a polia)?
Passo 1
E aí pessoaaaaaal, como vocês estão? Todo mundo bem?
Nessa questão temos um arranjo de fios e caixas, onde a caixa está apoiada sobre uma mesa e as caixas e estão penduradas por um fio. Igual mostrado na figura:
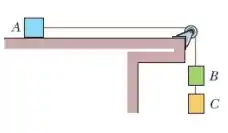
Foram dadas as massas de cada caixa, e precisamos determinar a tensão da corda que liga as caixas e .

Vamos desenhar o diagrama de forças nos blocos e para a partir daí escrevermos as equações força.
Passo 2
Em cada um dos blocos atuam as forças de tração dos fios (lembrando que fios diferentes provocam trações diferentes). Al��m disso, como os fios não mudam de tamanho, a aceleração das caixas precisa ser a mesma. Daí, temos:
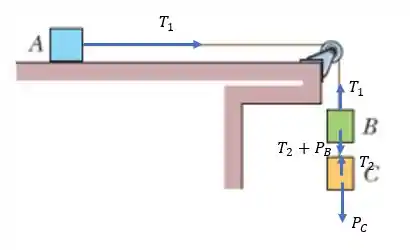
Usando a segunda lei de Newton , temos para a caixa :
Para
Para :
Temos equações e incógnitas, então podemos descobrir cada uma dessas variáveis 😊
Passo 3
Vamos substituir os valores numéricos dados no enunciado:
Isolando e na primeira e terceira equação, e substituindo na segunda vem que:
Portanto:
Daí, usando que:
Vem:
Prontinho! Essa é a tração que liga e .
Valeu genteeee!!