Um pintor está sobre uma plataforma suspensa por uma polia (figura). Puxando a corda em , ele faz a plataforma subir com aceleração . A massa do pintor é de e a plataforma tem . Calcule as tensões nas cordas e e a força exercida pelo pintor sobre a plataforma.
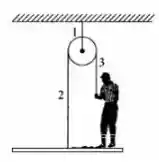
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um sistema envolvendo um pintor e uma plataforma que estão suspensos por uma polia:
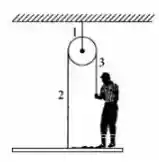
Quando o pintor puxa a corda em , a plataforma sobe com uma aceleração , onde .
Dessa forma, a questão nos pede para calcularmos as tensões nas cordas e e a força exercida pelo pintor sobre a plataforma.
E aí? Bora lá?
😉
Passo 2
Então... Fazendo o diagrama de corpo livre, vamos verificar as forças do sistema:
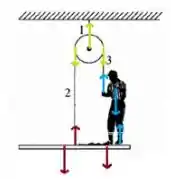
As forças em azul são as que estão atuando sobre o pintor, ou seja, a força peso do pintor , a tração da corda e a normal que a tábua exerce sobre ele.
Assim, aplicando a segunda Lei de Newton, temos:
Substituindo valores, temos:
Passo 3
Por outro lado, analisando as forças em marrom, temos:
Substituindo os valores, temos:
Dessa forma, temos o seguinte sistema:
Resolvendo o sistema, encontramos:
Lembrando que essa é a tração de e representadas na figura.
Para encontrar a força que o pintor exerce sobre a tábua, basta substituirmos no nosso sistema:
Passo 4
Como já descobrimos a tração em e , então podemos encontrar a tração em :
Entendeu direitinho? Responde aee ;)
