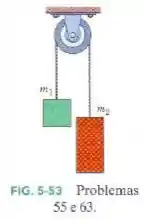
A Fig. 5-53 mostra dois blocos ligados por uma corda (de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa ; o outro tem massa . Quais são (a) o módulo da aceleração dos blocos e (b) a tensão na corda.
Passo 1
Pra gente resolver essa questão vamos ter que montar dois diagramas de corpo livre, um pra cada bloco e encontrar a equação para cada um deles. Após fazermos isso vamos ter um sistema que vai depender da tração no cabo e da aceleração do sistema, ao resolver o sistema resolveremos a questão.
A grande sacada de questões desse tipo é lembrar que a corda é inextensível, ou seja, ela tem um tamanho fixo. Quer entender melhor como isso funciona? Veja o desenho abaixo, da máquina em um instante, e em um pequeno instante depois.
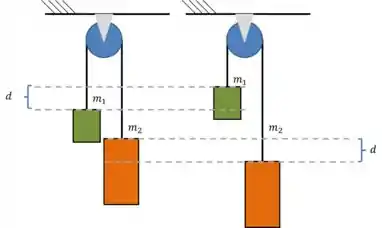
Percebeu? A mesma distância que subiu, desceu. Daqui a gente pode ver que a aceleração do bloco verde é para cima e a do bloco laranja é para baixo, você pode ver isso simplesmente pela massa de cada bloco.
Se os fios são inextensíveis é possível prova uma relação entre as acelerações mas como a dedução dela não é o foco vamos voltar nossa atenção para guarda-la, a relação é essa aqui:
O que significa que elas tem mesmo módulo mas sentidos opostos!
Passo 2
Faremos agora o diagrama de corpo livre de cada um dos dois blocos, lembrando que, por ser o mesmo fio que liga os blocos, a tensão é igual.
Para o bloco de massa :
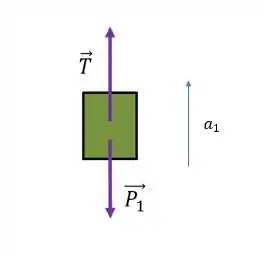
Vamos aplicar aqui a segunda lei de Newton e como esse bloquinho sobe o sentido pra cima será adotado como positivo para ele:
Temos:
Substituindo os valores de e , e chamando o módulo em comum das acelerações de :
Temos então a equação do primeiro bloco, vamos encontrar a do segundo.
Passo 3
Para o bloco de massa faremos o mesmo processo, começando pelo DCL:
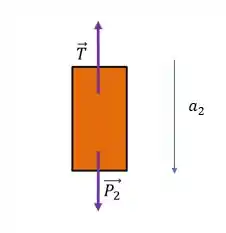
Seguindo a mesma lógica do outro bloco vamos tomar como positivo o sentido da aceleração, assim podemos aplicar a segunda lei de newton:
Substituindo os valores de , , e sabendo que :
Encontramos a equação do segundo bloco, hora de montarmos o sistema.
Passo 4
Temos agora, então, um sistema com duas equações que dão a resposta das letras a e b:
Somando as duas equações a gente vai ter o seguinte:
Agora pra encontrar a tração é só a gente voltar em qualquer uma das duas equações e substituir , aqui escolherei a primeira.
Achamos então: