Na figura, o fio e a roldana são ideais, e o plano fixo em que se apoia o bloco possui inclinação com a horizontal. Em todas as situações abaixo, o fio permanece tensionado e , mas o bloco pode variar. Quando necessário substituir valores, use .
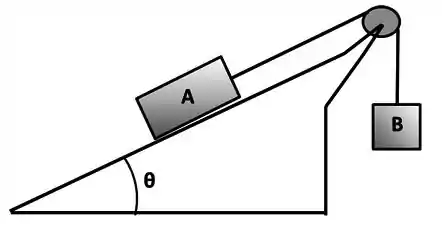
Neste item, despreze o atrito e suponha que o bloco possui aceleração para baixo. Represente o diagrama das forças que atuam sobre cada bloco e escreva as equações de movimento para ambos (deixe as equações literais e não as resolva).
Neste item, despreze o atrito e considere . Se o sistema parte do repouso e nos primeiros o bloco atinge a velocidade de para baixo, calcule a tensão no fio e a inclinação do plano.
Passo 1
Vamos começar fazendo o diagrama das forças, comumente chamado por nós de diagrama do corpo livre DCL. Vamos primeiro analisar o bloco , nele atuam:
- Força peso do bloco
- Normal que a plataforma faz no bloco
- Tração do fio
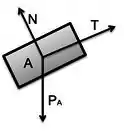
Utilizando para o bloco , um eixo que seja inclinado assim como a plataforma, teremos as seguintes equações:
Em :
Em :
No bloco , atuam:
- Força peso do bloco
- Tração do fio

Para o bloco , utilizaremos um eixo que esteja paralelo ao solo, dessa forma, temos:
Perceba que os blocos ficam submetidos à mesma aceleração, pois existe um vínculo entre eles, no caso, o fio!
Passo 2
Já temos as equações de movimento dos blocos, pois as encontramos no item anterior. Precisamos somente impor as condições do enunciado. Ele nos dá a massa do bloco , e além disso, nos diz que o bloco atinge uma velocidade de para baixo em . Portanto, podemos calcular a aceleração dos blocos. Se liga!
Sabendo que o bloco parte do repouso, temos:
Retomando as equações de movimento dos blocos achadas anteriormente, temos:
Somando as duas equações, temos:
Substituindo os valores dados, temos:
Utilizando somente a equação de movimento do bloco , podemos achar o valor da tração, dá uma olhada!
Substituindo os valores, temos:
Resposta
Ver figuras acima.
- Equações do bloco :
- Equação do bloco :
;