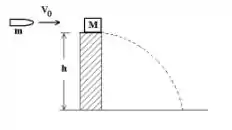
Uma partícula de massa e velocidade de é disparada contra um bloco de massa como mostra a Fig.(3). O bloco se encontra em repouso na borda de um poste de altura de . Considerando que o coeficiente de restituição , determine (a) as velocidades após a colisão (b) Determine a velocidade em que o bloco atinge o solo, desprezando a resistência do ar.

Agora, temos um sistema de duas equações com duas incógnitas:

Podemos resolver esse sistema para encontrar v1 e v2.

Multiplicando a segunda equação por 4 e somando à primeira equação:

Agora, podemos usar a segunda equação para encontrar v1:

Portanto, após a colisão, a partícula tem uma velocidade de 2,27m/s para a direita, e o bloco tem uma velocidade de 3,47m/s para a direita.

Para determinar a velocidade com que o bloco atinge o solo, desprezando a resistência do ar, podemos usar a equação das leis do movimento uniformemente acelerado. Nesse caso, a única força atuando sobre o bloco é a gravidade, que gera uma aceleração constante.

A equação de movimento para queda livre, desprezando a resistência do ar, é dada por:

Agora, podemos resolver essa equação para encontrar o tempo t que o bloco leva para cair a partir da altura de 1,4 metros:

Agora, como mencionado anteriormente, a velocidade horizontal do bloco se conserva, então a velocidade horizontal final (vx ) é a mesma que tinha após a colisão, ou seja, 3,47m/s.

Agora, podemos calcular a velocidade total (v) com que o bloco atinge o solo usando o teorema de Pitágoras, considerando a componente horizontal (vx ) e a componente vertical (vy ) da velocidade:

Já sabemos que vy é a velocidade vertical, que podemos calcular usando a fórmula da velocidade final em queda livre:

Agora, podemos calcular a velocidade total:

Portanto, a velocidade total com que o bloco atinge o solo, desprezando a resistência do ar, é de aproximadamente 6,28m/s, considerando tanto a componente horizontal quanto a vertical da velocidade.