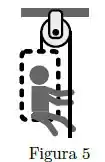
Uma pessoa está sentada em uma cadeira presa a uma corda de massa desprezível que passa por uma roldana de massa e atrito desprezíveis e desce de volta às mãos desta pessoa, conforme a Figura 5. Assuma que o peso total do sistema pessoa cadeira é . Para que a cadeira suba com velocidade constante, o homem deve puxar a corda com uma força de módulo igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(j)
(k)
Passo 1
Nessa questão, a pessoa sentada na cadeira está se puxando através da corda.
Queremos saber a força necessária para fazer a pessoa e a cadeira subirem com velocidade constante, ou seja, sem aceleração.
Mas olha aqui, lembra da lei de ação e reação?
Pela ação e reação, a força que a pessoa faz sobre a corda (puxar para baixo) é a mesma que a corda faz sobre a pessoa (puxar para cima).
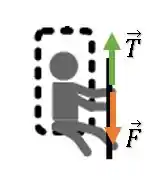
Então, basta achar a força de tração na corda que achamos a força que a pessoa faz.
Um detalhe importante é que a corda está ligada ao sistema pessoacadeira duas vezes, já que está presa à cadeira e à mão da pessoa.
Passo 2
Primeiro de tudo, se eles sobem sem aceleração, isso significa que há um equilíbrio de forças. Então, vamos analisar as forças aplicadas sobre o sistema pessoacadeira, tratando os dois como um corpo só.
Repare que nos dois pontos em que a corda está ligada ao sistema pessoacadeira vai existir uma força de tração sobre eles. Logo, o diagrama do corpo livre (DCL) fica assim:
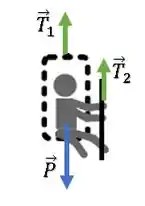
Se temos um equilíbrio de forças , podemos dizer que o somatório de forças nesse “corpo” é nulo:
Mas se liga aqui, se a polia e a corda são ideais, a tração sobre a corda em qualquer ponto será a mesma ,né?
Então, as forças e são iguais:
A força peso é , logo:
Achamos a força de tração na corda. Se a força de tração é igual em módulo à força que a pessoa faz, conseguimos a resposta:
Ou seja, marcamos a alternativa (b).
Resposta
Letra (b)