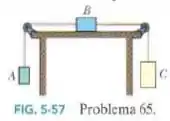
A Fig. 5-57 mostra três blocos ligados por cordas que passam por polias sem atrito. O bloco B está sobre uma mesa sem atrito; as massas são e . Quando os blocos são liberados qual é a tensão da corda da direita?
Passo 1
A saída aqui também é pensar no tamanho fixo dos fios que ligam os blocos e concluir que: o mesmo deslocamento que o bloco C tiver para baixo, o bloco B terá para direita e o bloco A terá para cima. O que, pensando nas acelerações, nos dá:
Passo 2
Podemos aplicar a segunda lei de Newton, junto com o Diagrama de Corpo Livre em cada um dos corpos, mas temos que lembrar que temos dois fios diferentes, portanto, chamaremos de a tração do fio da esquerda e de a tração do fio da direita.
No bloco C, analisando somente as forças na vertical, já que seu movimento se limita a esse eixo:
Substituindo os valores conhecidos:
)
Já no bloco B, analisaremos somente as forças na horizontal:
Substituindo os valores conhecidos:
E finalmente, no bloco A, analisando só na vertical de novo:
Substituindo os valores conhecidos:
Passo 3
Para encontrar a aceleração , faremos:
E obteremos:
Para chegarmos a resposta do problema, o valor da tensão , substituiremos o valor de na Eq.1: