Na figura , os blocos estão ligados por fio e roldana ideais e podem deslizar sem atrito sobre as paredes do carrinho de massa . Qual o valor da força, aplicada ao carrinho, a partir do repouso, que faz com que fique parado em relação a ?
Passo 1
Eaew, tudo certinho contigo?
Temos o seguinte diagrama de forças para o problema apresentado
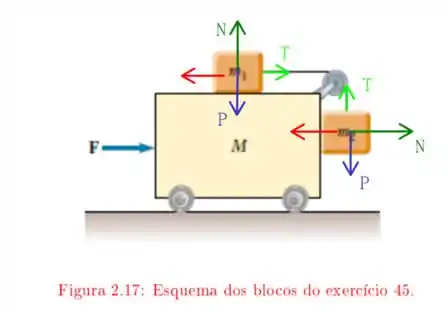
As forças em vermelho surgem devido a ação da força sobre o carrinho. Vamos usar esses diagramas e as leis de Newton para identificar qual deve ser o valor de nossa força! Ambos os blocos menores tem a mesma massa , o carrinho tem massa , a roldana é ideal e os fios inextensíveis. Vamos tentar usar essas informações agora! Saca só!
Passo 2
Primeiro, vamos considerar a atuação da força em todo o corpo, de forma que
note que
Ou seja, precisamos que visto como um sistema isolado, sofra a influência de uma “força” que gere uma aceleração contrária à . Essa “força” é a força em vermelho indicada em nosso sistema! Vamos analisar o corpo de massa individualmente!
Passo 3
Horizontalmente, as forças atuando sobre são
a força fictícia tem o mesmo módulo que a força , mas a aceleração gerada é tal que
de forma que a relação se torna
queremos que o corpo seja visto no equilíbrio, portanto, , e assim, temos que
como temos que
Portanto, a tensão deve ser dada por
Mas queremos a aceleração, portanto, vamos procurar a tensão!
Passo 4
Do segundo corpo, podemos obter que
ou seja, podemos escrever que
O módulo dessa aceleração pode ser usado para escrever a força aplicada como
A questão foi essa! Te vejo na próxima! Tchau Tchau!