Um carro de massa trafega com velocidade de módulo constante na direção leste inicialmente. Ele então entra numa curva de raio constante na posição da figura. No final da curva (posição ) o carro passa a trafegar na direção norte. O comprimento da curva é de . O carro completa o percurso da curva em . Os coeficientes de atrito estático e cinético entre os pneus do carro e o asfalto da curva são respectivamente e .
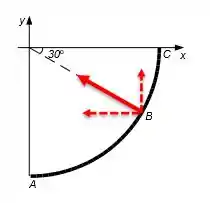
(a) Calcule a aceleração do carro quando ele está na posição em termos dos vetores unitários e .
(b) Calcule em termos dos vetores unitários e as forças de atrito que agem sobre os pneus do carro no início e no final da curva, posições e .
Passo 1
(a)
Sabemos que o comprimento do arco é dado por:
E então, descobrimos o raio da curva:
Para descobrirmos a velocidade, é só usar a fórmula da velocidade média:
E finalmente, a aceleração que atua no carro é a aceleração centrípeta, dada por:
Decompondo em vetores:
- ''Passo 2
(b)
Em , a força que atua no carro é a força centrípeta, dada por:
Vetorialmente:
Já para o ponto , só muda a direção, que fica horizontal:
Resposta
a)
b) Em A:
Em C: