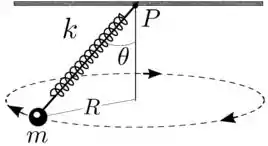
Uma partícula de massa é suspensa por uma mola ideal de constante elástica presa no teto. A particula gira em movimento circular uniforme horizontal, de raio e centrado na vertical que passa pelo ponto de suspensão da mola no teto, como indica a figura. A mola mantém-se reta e distendida de um comprimento (a ser determinado). A reta que passa pelo ponto de suspensão da mola e a particual mantém um ângulo constante com a vertical, descrevendo uma superfície cônica no espaço. Considere como dados , , , e o módulo da aceleração da gravidade.
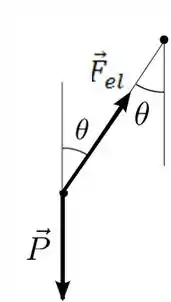
- Represente em um diagrama as forças que agem sobre a partícula em um instante arbitrário.
- Calcule a distensão da mola.
- Determine o módulo da velocidade da partícula.
Passo 1
Vamos primeiro escrever os dados do problema
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
Vamos agora fazer o DCL
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Não, o bloco não está apoiado em nenhuma superfície.
Não, não existe fio atuando.
Sim, existe uma mola.
Não, não existe atrito
O DCL fica
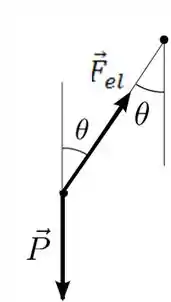
Passo 3
b)
Como ele está em um movimento circular, com o centro apontando na horizontal, ele está em equilíbrio no
Devemos encontrar a sua componente vertical usando a “regra do COlado, SEparado”.
Teremos
Passo 4
c)
Vamos agora fazer a analise no , isso porque a força que aponta para o centro será a força centrípeta
Devemos encontrar a sua componente vertical usando a “regra do COlado, SEparado”.
Teremos
Usando o valor que achamos para