Uma moeda se encontra a uma distância do eixo de um disco que se encontra numa posição plana e tem raio . O coeficiente de atrito estático entre o disco e a moeda é . Suponha que a velocidade angular do disco aumenta de forma constante a partir do repouso. Qual será o módulo de sua velocidade angular no instante em que a moeda iniciará a escorregar?
Passo 1
Primeiro vamos analisar as forças que estão agindo na nossa super moeda, ok?
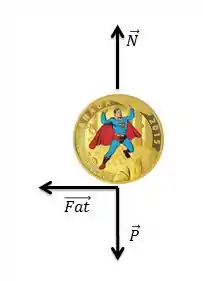 ,
,
Agora que já sabemos as forças que atuam nela e sabemos que, como o movimento é na horizontal, é a força de atrito que está atuando como força centrípeta. Como ele vai estar na iminência de escorregar, vamos saber que a é máxima!
Passo 2
Primeiro vamos calcular a força de atrito máxima, e depois vamos igualar à força centrípeta para descobrirmos a velocidade angular.