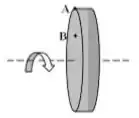
Dois pontos estão localizados sobre uma roda rígida que está girando com uma velocidade angular decrescente em torno de um eixo fixo. O ponto está localizado na borda da roda e o ponto está a meio caminho entre a borda e o eixo. Qual das seguintes afirmações referentes a esta situação é verdadeira?
- Ambos os pontos possuem a mesma aceleração centrípeta.
- Ambos os pontos possuem a mesma aceleração tangencial.
- A velocidade angular no ponto é maior do que a velocidade angula no ponto .
- Ambos os pontos possuem a mesma velocidade angular instantânea.
- A cada segundo o ponto gira de um ângulo maior do que o ponto .
Passo 1
Bem, vamos começar analisando o movimento dos pontos.
A rotação do disco é igual para ambos os pontos, logo a distancia angular para ambas é a mesma.
Passo 2
Agora seguimos para o que faz o movimento rotacional: a aceleração centrípeta. Bem, sabemos que . Como o varia entre os pontos, não podemos afirmar que a aceleração centrípeta é a mesma.
Passo 3
Mas e a velocidade, é a mesma? Bem, como também já sabemos, . O raio nós já vimos que é diferente entre os pontos.
Mas e a velocidade angular ?
Temos que . Logo, a velocidade angular de ambos os pontos só depende da frequência de rotação, tornando-a constante em todos os pontos do disco.
Sabendo que varia e que permanece constante, podemos tirar uma conclusão sobre a velocidade : varia de acordo com o ponto.
Passo 4
Até aqui, temos que a letra a) é falsa, a letra c) é falsa, a letra d) é verdadeira e a letra e) é falsa. Já podemos responder com certeza a questão.
Mas vamos entender a afirmativa que resta: ambos os pontos possuem a mesma aceleração tangencial.
A velocidade é decrescente, conforme o enunciado, logo temos uma aceleração tangencial negativa. Bem, ambas tem que parar no mesmo instante, certo? E a velocidade de é diferente da velocidade de , certo? Conclusão, a taxa de desaceleração para tem que ser diferente da taxa de desaceleração para .
Resposta
Letra d)