Questão 3). Um disco de metal de massa descreve uma circunferência horizontal de raio sobre uma mesa sem atrito, de altura , enquanto permanece ligado a um cilindro de massa pendurado por uma corda inextensível, de massa desprezível, que passa por um furo no centro da mesa, conforme representa a figura ao lado (sem escala). O disco () se move com velocidade constante, em módulo, para manter o cilindro () em repouso. A corda se rompe e o disco de massa é lançado horizontalmente, chegando ao solo depois de percorrer uma distância horizontal . Sabendo que e que o alcance é o dobro da altura da mesa , determine o raio da circunferência descrita pelo disco antes da corda se romper. Escreva sua resposta em termos de . 🤔
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

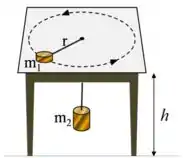
Nessa questão temos dois discos, um de massa em cima de uma mesa sem atrito de altura e outro de massa , eles estão presos por uma corda de massa desprezível, inextensível que passa por um furo no meio da mesa.
O disco está descrevendo movimentos circulares constantes enquanto o disco está parado e pendurado na outra extremidade da corda.
Após um tempo, a corda se quebra, os discos são separados e o disco é lançado de cima da mesa percorrendo uma distância horizontal .
Além disso, foi dito que a massa é vezes , ou seja, . E também que é o dobro de , logo,
Grandinha, não é? 👀
O que queremos saber é: qual era o raio do movimento inicial do disco (em termos de )?
Tem ideia de como obter esse valor?? 🤔🤔
Bora ver! 😁
Passo 2
Primeiramente o sistema estava em equilíbrio já que o disco estava parado no ar (suspenso pela corda). Se estava parado, a resultante das forças que agiam sobre ele era .

Analisando as forças que atuam nos discos vemos que a força peso puxa para baixo e consequentemente puxa em direção ao centro da mesa.
As forças de tração na corda se cancelam então para esse sistema estar em equilíbrio, dizemos que a força centrifuga (o mesmo vetor que a com o sentido oposto) cancela a força peso .
Perceba que se eles fossem diferentes, o disco não ficaria parado.
Logo
O que é a força centrípeta? Sabemos que essa força é dada por
( = aceleração centrípeta)
E a força peso é dada por
Se , substituindo por em , então
Tranquilo até aqui? 😎
Passo 3
Vamos isolar em um lado da igualdade,
Queremos obter em função de , então vamos investigar mais um pouquinho.
Após a quebra da corda, o disco é lançado de cima da mesa resultando em uma trajetória oblíqua.
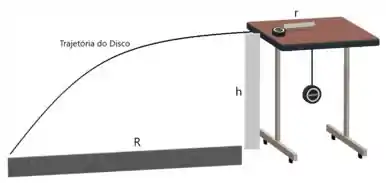
Em um lançamento obliquo, o objeto é composto por duas componentes de velocidade.
Horizontalmente a velocidade é constante e verticalmente a velocidade é variável com a aceleração apontando para baixo devido à gravidade.
Voltando a equação de , vemos que a velocidade da aceleração centrípeta se transforma na velocidade horizontal do movimento, ou seja, agora vamos tratar como
Se horizontalmente o movimento é constante, então podemos dizer que a velocidade é o espaço percorrido dividido pelo tempo.
No enunciado foi dito que vale . Fazendo essa substituição, temos
Entendeu essa parte? 😁
Passo 4
Já verticalmente podemos usar a formula
O espaço vertical percorrido corresponde à altura da mesa, ou seja, a .
Inicialmente a velocidade em é já que o disco parte de uma superfície horizontal.
A aceleração nesse caso é dada pela aceleração gravitacional (vamos considerar positivo).
Fazendo essas substituições, temos
isolando em um lado da equação
Elevando os dois lados de ao quadrado, temos
Como , então
Substituindo em
Simplificando a equação
Interessante, não é? 😎
Passo 5
Substituindo em , vamos obter
Outra informação importante é que foi dito que , logo podemos afirmar que
Com isso, vemos que
Assim chegamos ao resultado de que o raio que percorre inicialmente deve ser de !
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
