Um viciado em movimento circular, com de massa, passeia em uma roda-gigante que descreve uma circunferência vertical de de raio a uma velocidade escalar constante de .
- Qual é o período do movimento?
Qual é o módulo da força normal exercida pelo assento sobre o viciado quando ambos passam
(b) pelo ponto mais alto da trajetória circular e
(c) pelo ponto mais baixo?
Passo 1
Oi pessoal, tudo bem? Vou ajudar você aqui! Vamos começar?
Letra (a):
Aqui o problema pede para calcular o período e a força normal. A ideia é relembrar das fórmulas que dao essas duas quantidades:
Então galera , nós sabemos queo período pode ser obtido através da relação :
Passo 2
Letra (b): agora o problema pede para calcular a força normal quando eles passam no ponto mais alto da trajetória, então precisamos fazer um diagrama de forças:
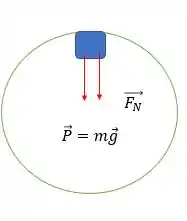
A resultante deve ser a força centrípeta, então:
Bom pessoal , nós sabemos que no ponto mais alto do percurso:
Beleza?
 vamos cacular a normal no ponto mais baixo? Partiu?
vamos cacular a normal no ponto mais baixo? Partiu?
Passo 3
Letra (c):
No ponto mais baixo:
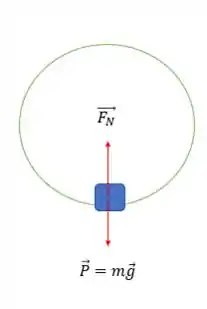
Por outro lado , no ponto mais baixo do percurso :
Tranquilo? E é isso! Espero ter ajudado!