Você está dirigindo um carro em uma pista circular de raio , que é inclinada de um ângulo com a horizontal, como indicado na Figura. A velocidade do carro é , constante em módulo.
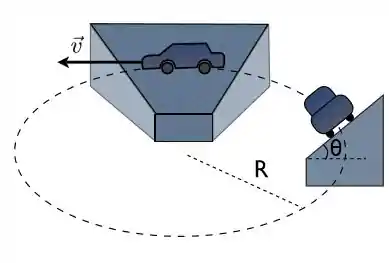
(a) Faça um diagrama de forças considerando que não existe nenhum tipo de atrito entre os pneus do carro e a pista.
(b) Calcule a velocidade na ausência de atrito em função de , e .
(c) Considerando que mesmo com o carro andando há uma força de atrito do tipo estático (de coeficiente ) entre os pneus do carro e a pista, que evita que o carro deslize para baixo ou para cima. Faça o diagrama de forças nestes dois casos.
(d) Com o atrito descrito no item (c) entre o pneu do carro e a pista, determine a velocidade mínima e máxima que o carro pode ter para que este não deslize.
Passo 1
(a)
Sem a força de atrito teremos apenas a força normal e a força peso , formando uma força resultante centrípeta .
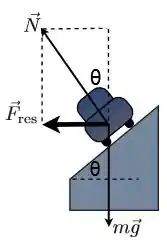
Passo 2
(b)
No caso sem atrito, temos que a componente vertical da força normal compensa exatamente a força-peso, portanto:
A força resultante será na horizontal, e será a componente horizontal da normal:
Usando , e a fórmula da aceleração centrípeta: , temos que:
Passo 3
(c)
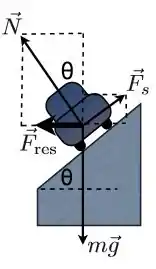
Se o carro andar a baixa velocidade, ele correrá o risco de deslizar para baixo na pista. Logo ele precisa de uma força de atrito que o empurre para cima na pista. Ficará assim:
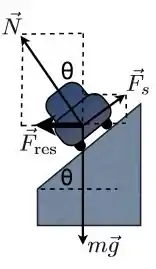
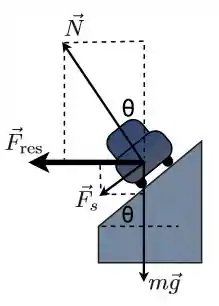
Além disso, o carro poderá andar a altíssima velocidade e correr o risco de sair para fora da pista. Para isso a força de atrito terá que empurra-lo de volta a pista. Então teremos também este caso:
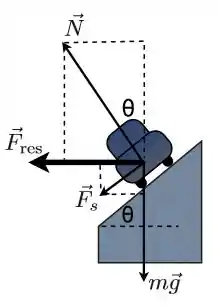
Passo 4
(d)
Lembra que no item calculamos a velocidade do carro na pista sem atrito? Então, está velocidade é a referência para dizer se está a uma velocidade alta ou baixa. A força de atrito estático será para cima da pista se , ou para baixo da pista no caso de .
Vamos supor inicialmente o primeiro caso, de uma velocidade abaixo daquela na qual o atrito seria nulo. Temos então, pelo diagrama do item anterior, que as componentes na horizontal e na vertical são dadas por:
Na horizontal:
Na vertical:
Usando que o valor máximo da força de atrito estático é , da segunda equação encontramos que o valor máximo da normal é:
Substituindo esse resultado na primeira equação, temos que:
Como:
Obtemos:
O caso em que é totalmente análogo ao anterior, bastando que se inverta o sentido da força de atrito nas equações acima. O resultado é a mudança no sinal de :
Resposta
(a)
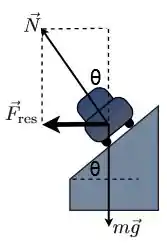
(b)
(c) Baixa velocidade:
Alta velocidade:
(d)