Um carro trafega com velocidade constante de módulo , numa estrada curva e inclinada de ângulo com a horizontal. A massa do carro é e o raio da curva é . A velocidade para se fazer a curva sem a ação do atrito é igual a . Os coeficientes de atrito estático e cinético entre os pneus e a estrada são respectivamente e . O desenho abaixo mostra uma vista frontal do carro e da curva inclinada.

Utilize: e .
(a) Faça o diagrama de corpo livre para o carro nesta situação sabendo que o carro faz curva com velocidade igual a . Utilize para a aceleração da gravidade.
(b) Utilizando notação literal, escreva a segunda lei de Newton na forma vetorial e por componentes para esta situação. Especifique as direções envolvidas na decomposição dos vetores.
(c) Sabendo que o módulo da força centrípeta que age sobre o carro nesta situação é igual a , calcule o módulo da força de atrito que age sobre o carro.
Passo 1
O que acontece de diferente quando o carro realiza uma curva sobre uma rampa inclinada?
A força normal é sempre perpendicular à superfície, então com a inclinação ela ficará assim:

Assim, a componente horizontal da força ficará na direção do centro da curva...
Logo a força normal “ajuda” o carro a fazer a curva, pois o papel de força centrípeta na fica apenas com a força de atrito, como é o caso de uma pista plana.
Passo 2
Na letra (a), queremos o diagrama de forças.
A força será para baixo e a força será perpendicular à pista.
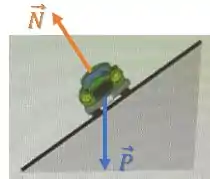
E a força de atrito aponta para cima ou para baixo da rampa?
Ele nos disse que quando o carro realiza a curva à , não há força de atrito nenhuma.
Isso acontece porque a componente horizontal da força normal já é suficiente para atuar como força centrípeta nessa velocidade.
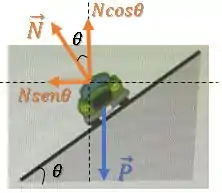
Porém dá uma olhada na expressão da força centrípeta:
Então se diminuirmos a velocidade , a força centrípeta resultante deve ser menor que somente a componente da normal .
Então, a força de atrito deve ter uma componente para “fora da curva” para a direita, logo, aponta para cima da rampa.
O diagrama de forças fica assim:
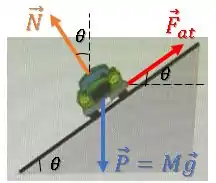
Quando a velocidade é baixa (menor que ), a tendência de deslizamento do carro é para baixo, logo a força de atrito aponta para cima.
Se a velocidade fosse mais alta (maior que ), a tendência de deslizamento do carro é para cima, logo a força de atrito aponta para baixo.
Passo 3
Na letra (b), queremos a segunda lei de Newton na forma vetorial e depois as equações para cada direção.
A segunda lei de Newton é a seguinte:
Quando estamos trabalhando com vetores, o vetor da força resultante é a soma vetorial de todos os vetores das forças:
Então na forma vetorial, temos:
Passo 4
Agora, vamos escrever a segunda lei de newton para cada direção.
Vamos decompor os vetores nas componentes horizontais e verticais.
Escolhemos essas direções porque a aceleração resultante (centrípeta) aponta para o centro da curva, ou seja está na direção horizontal.
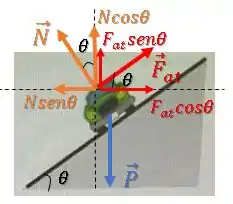
Na direção horizontal, a força resultante é igual à força centrípeta, logo:
Enquanto na direção vertical, o carro apresenta equilíbrio de forças:
Passo 5
Na letra (c), queremos a força de atrito sobre o carro, sabendo que a força centrípeta vale .
Então, nossa equação de forças na horizontal fica assim:
Temos que resolver esse sisteminha aqui:
Vamos tentar nos livrar dessa força normal para encontrar o valor de .
Isolando os para um lado da equação, temos:
Vamos dividir a primeira equação pela segunda:
Multiplicando cruzado, temos:
Sendo :
Substituindo os valores, temos:
Resposta
(a)
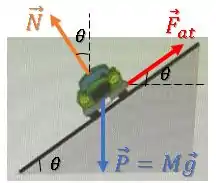
(b)Segunda lei de Newton vetorial:
Direção horizontal:
Direção vertical:
(c)