Determine a equação da reta tangente à curva no ponto .
Passo 1
Escolher a equação da reta
Quando caímos numa questão de reta tangente, a primeira coisa que deve piscar na nossa cabeça é: opa, preciso saber a equação da reta! Tem duas possíveis:
Nós vamos usar aqui a segunda, beleza? Isso porque o ponto é um ponto de tangência e como isso é dado do problema, já ficamos com:
Falta só lembrar quem é o . O valor de nada mais é do que a derivada de no ponto de tangência. Logo:
Passo 2
Realizar derivada implícita
Seria bem mais fácil se tivéssemos uma função bem definida, não é? Como não é o caso, vamos partir pra derivação implícita mesmo. Derivando dos dois lados por em relação a , temos:
No ponto de tangência , vamos ter:
Opa, da pra simplificar isso, vamos lembrar que:
Partiu então:
Passo 3
Montar a equação da reta e olhar que lindo não fica no gráfico
Agora que sabemos o valor de , basta colocar ele na equação da reta, que vai ficar então:
Graficamente, temos:
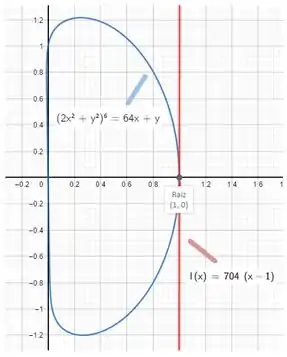
Olha só! Olha lá! A reta tangente é quase que vertical nessa imagem! Admite, comprovação gráfica deixa tudo mais bonito!