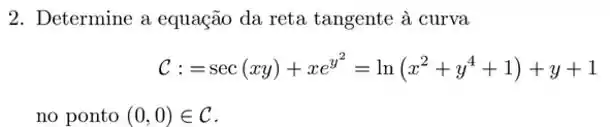
Passo 1
Repara, se queremos a reta tangente à curva dada no ponto , significa que ela passa nesse ponto aí. Bom, com isso a gente já sabe que se a reta for modelada por , o seu coeficiente linear vai valer . Afinal, aplicando o ponto na reta, teríamos:
Assim, basta achar a derivada de no ponto dado e usá-la como para ter a nossa reta , onde temos
Passo 2
Derivamos a função implícita agora usamos a Regra da Cadeia e do Produto:
Passo 3
Agora, aplicando , teremos:
Logo, a reta será:
Resposta
Exercícios de Livros Relacionados
Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. y 2 y 2 - 4 = x 2 ( x 2 - 5 ) , ( 0 , - 2 ) (curva do diabo)
Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + y 2 = 2 x 2 + 2 y 2 - x 2 , 0 , 1 2 (cardioide)
Encontre as equações de ambas as retas tangentes para a elipse x 2 + 4 y 2 = 36 que passem pelo ponto ( 12 ,3 ) .
Duas curvas são ortogonais se suas retas tangentes forem perpendiculares em cada ponto de interseção. Mostre que as famílias dadas de curvas são trajetórias ortogonais uma em relação à outra, ou seja,
28. Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + 2 x y - 4 y ² = 12 ² , ( 2,1 ) (elipse)