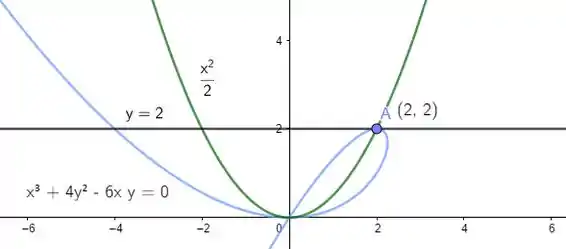
Determine os pontos da curva
Com coordenada , onde a reta tangente é paralela ao eixo
Passo 1
Opa, vamos lá. A questão ta pedindo pra gente achar pontos de tangência. Show, só que tem um detalhe: a reta tangente a esse ponto não é uma reta qualquer, e sim uma reta paralela ao eixo , que nada mais é do que uma função constante! Logo, se a equação da reta tangente for:
Então nesse a inclinação da reta tangente, que é o , vai ser igual à ! E como a inclinação da reta tangente é dada pela primeira derivada, vamos então caçar na nossa curva os pontos em que:
Passo 2
Eita, mas a curva não ta explícita da forma , e agora?
Caaaaalma gafanhoto, se ela não está explícita, vamos derivar implicitamente em relação a mesmo que dá certin, quer ver? Saca só:
Ficamos com:
Mas como vimos, nesse caso vai ter que ser . Temos então:
Passo 3
Caraca o resultado não foi ainda um ponto, como o enunciado pediu, e sim uma curva. Mas relaxa, não é o fim do mundo porque sabemos que os pontos de tangência também estão sobre essa curva
Vamos juntar então essa curva com a do enunciado, beleza? Se:
Então juntando as duas curvas temos:
Agora sim começamos a nos aproximar da resposta final. Dá uma olhada, pra
Podemos ter ou que ou que ! Usando esses valores de , temos, pra
E pra :
Os pontos vão ser então:
Maravilha, só falta uma coisa: descartar o primeiro ponto. O enunciado pediu pra gente só pontos em que então, no caso, só sobrou um! Questão resolvida galera!
Resposta
Ponto