. Um automóvel descreve uma curva com inclinação como indicado na figura. O coeficiente de atrito estático é e o raio da trajetória circular é . Nestas condições o automóvel pode se manter na curva sempre que sua velocidade escalar esteja dentro de certos valores máximos e mínimos. Determine a velocidade mínima com a qual o carro pode fazer a curva sem deslizar.
Passo 1
Vem comigo que a gente detona essa questão!
Como o automóvel descreve uma curva, ele querendo ou não está realizando um movimento circular, logo temos que ter uma força centrípeta que aponta para o centro da curva (no caso a direção ).
Então a resultante das forças que atuam na direção tem que ser igual a essa força centrípeta, dada por:
E é daí que tiramos a velocidade. Para encontrar a velocidade mínima para o carro não derrapar, teremos que analisar as forças que agem nesse carro, sendo que a força de atrito deve ser máxima para que encontremos a velocidade mínima.
Para vermos melhor o que acontece vamos desenhar um diagrama de corpo livre.
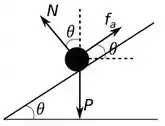
Tendo esse digrama, podemos usar a segunda lei de Newton na direção e , para analisar nossas forçar e ir atrás da velocidade do carro.
Passo 2
Começando com a direção , já que a força resultante nessa direção deve ser zero, temos:
Usando que , temos
Guarda isso que a gente vai precisar.
Passo 3
Agora na direção , temos que a força resultante é:
Usando o fato de que , com isso temos:
Passo 4
Agora vamos isolar .
Substituindo os valores que conhecemos, temos:
Assim temos que:
Essa é a nossa velocidade mínima.