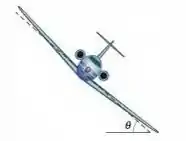
(Cap 6 – Ex 53) Um avião está voando em uma circunferência horizontal com uma velocidade de (Fig. 6-41). Se as asas estão inclinadas de um ângulo com a horizontal, qual é o raio da circunferência? Suponha que a força necessária para manter o avião nessa trajetória resulte inteiramente de uma "sustentação aerodinâmica" perpendicular à superfície das asas.
Passo 1
Faaaala, cê tá bem?
Então, a gente em um avião fazendo um movimento circular horizontal. Se tem movimento circular, tem aceleração centrípeta na direção horizontal, apontando para o centro da trajetória. No caso da figura, apontando para a direita.
Aí o que ele quer é o raio da trajetória circular do avião.
Ele diz que há uma força de sustentação que é perpendicular às asas do avião, temos também a força peso do avião para baixo. Então galera, a boa desse exercício é construir o diagrama de corpo livre do avião, já que a gente tem essas forças atuando:
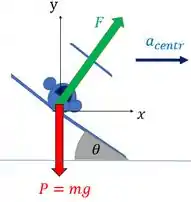
Percebe que a força que tem componente na direção horizontal é a força de sustentação. Então a componente horizontal dela vai fazer o papel de força centrípeta, produzindo aceleração centrípeta e mantendo o avião na trajetória circular.
Já a componente vertical de vai ser responsável por manter o avião no ar, se oponto a força peso.
O que a gente pode fazer aqui é usar a segunda lei de Newton nesse avião para achar equações que possam nos dar uma expressão para o raio dessa trajetória circular. Bora lá ver como fazer isso!
Passo 2
Primeiros vamos achar as componentes de . O que temos que fazer aqui é decompor essa força no eixo vertical e no eixo horizontal
Só que pra gente fazer essa decomposição precisamos saber qual o ângulo formado dessa força com a horizontal! Pra isso vamos fazer um esquema dos ângulos:
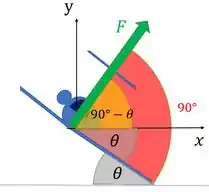
Já que é perpendicular ao avião, esse ângulo rosa precisa ser de , então o ângulo que faz com o eixo vai ser , onde .
Isso significa que as componentes e de são dadas por
Percebe que a gente usa cosseno para componente porque o nosso ângulo está colado no eixo . E aí na outra componente usamos .
Passo 3
Vamos aplicar a segunda lei de Newton na vertical:
Não há movimento nessa direção, então . Ficamos assim:
Substituindo as expressões de cada uma dessas forças:
Passo 4
Agora para o eixo :
Temos que a aceleração nesse caso é a aceleração centrípeta que tem a fórmulinha
E a única força atuando é a componente de , . SUbtituindo essas duas coisinhas:
Passo 5
Temos duas equações:
Como queremos o raio da trajetória vamos dividir uma equação pela outra
Isolando :
Agora é só substituir os valores! Mas aaaantes vamos converter a nossa velocidade para
Agora sim, substituindo:
Show! :D
Resposta
Traquilo pessoal???? Bora resolver mais questões então!!!!!!!