Parte I:
Um corpo de massa suspenso por um fio de comprimento , que faz um ângulo com a vertical, gira descrevendo uma circunferência de raio . Esse dispositivo é designado pela expressão pêndulo cônico.
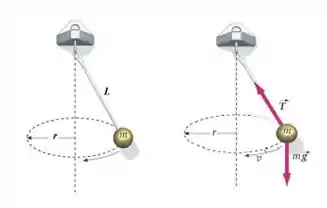
(a) Obtenha uma expressão literal para o período desse pêndulo em função de , e . A expressão pode conter , desde que seja indicada outra fórmula para calculá-lo em termos das grandezas pedidas.
(b) Considere , e . Calcule o período desse pêndulo.
Passo 1
Um pêndulo cônico nada mais é do que um pêndulo simples só que em vez de transladar de um lado para o outro, faz um movimento circular uniforme sempre à uma mesma altura.
Se a velocidade da partícula é constante na trajetória do círculo, ela vai ter um mesmo intervalo de tempo para completar cada volta, ou seja um período .
A questão gira em torno desse período, que vai ter o nome de .
Passo 2
(a) Obtenha uma expressão literal para o período desse pêndulo em função de , e . A expressão pode conter , desde que seja indicada outra fórmula para calculá-lo em termos das grandezas pedidas.
Para encontrar uma expressão para o período , vamos relacionar as forças com a velocidade da partícula através da expressão de força centrípeta.
Primeiro, vamos decompor a força de tração na direção vertical e horizontal:
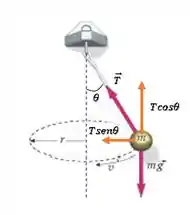
Fazemos isso, porque além de conseguir fazer o somatório de forças na vertical, temos uma componente da força apontando para o centro da trajetória circular, ou seja, fazendo o papel da força centrípeta .
A expressão da força centrípeta é dada por:
Onde é o raio do círculo.
Então, vamos igualar a componente com a força centrípeta, sendo o raio do círculo :
Além disso, o somatório de forças na vertical nos dá:
Agora, vamos juntar as equações e , dividindo por :
Se não pensou em juntar dividindo, relaxa! Você também poderia ter juntado as duas substituindo, por exemplo a tração , e chegaria no mesmo resultado.
Passo 3
Achamos uma relação para a velocidade da partícula. Mas, lembra que ela faz um (MCU)?
Então, podemos dizer que sua velocidade (sempre constante) é dada por:
Em um intervalo de um período , a partícula percorre uma volta no círculo, então:
Passo 4
Vamos relacionar a expressão do Passo 2 com a velocidade da partícula:
Isolando o período :
Por último, devemos achar quem é para que a nossa resposta fique apenas em função de , e .
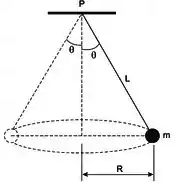
Podemos dizer que:
Então, o nosso ângulo vai ser:
Então, achamos finalmente o período:
É meio feiosa essa expressão mesmo. Mas, se preferir o enunciado afirma que podemos deixar em função de e mostrar como calculá-lo. Então, poderíamos ter parado nessa resposta também:
Passo 5
(b) Considere , e . Calcule o período desse pêndulo.
Como já temos a expressão para calcular , basta substituir os valores dados:
Resposta
(a) ou
(b)