Parte II:
A inclinação de em uma curva com raio na pista de corrida de carros permite que atinjam a velocidade máxima de sem derrapar para fora da pista. Admita o valor de para a massa de um desses carros. Suponha o carro como uma partícula.

(c) Determine o coeficiente de atrito estático dos pneus com a pista.
Passo 1
Imagine que o carro vai aumentando de velocidade cada vez mais. Uma hora ele vai acabar derrapando para fora da curva, não é mesmo?
Ou seja, sua tendência de deslizamento é para cima na rampa. Logo, a força de atrito vai apontar para baixo (contra a tendência de deslizamento).
A questão pede pra gente determinar o coeficiente de atrito estático quando o carro está à nessa determinada pista.
OBS: Se o carro está em movimento, porque estamos falando de atrito estático? Será atrito estático pois o ponto de contato do pneu com o solo estará parado (não arrasta).
Passo 2
Para achar esse coeficiente de atrito, vamos relacionar as forças com a velocidade do carro usando a expressão da força centrípeta.
Para isso, vamos decompor as forças nos eixos horizontal e vertical (para onde aponta a aceleração). Ou seja para o centro do círculo que o carro percorre.
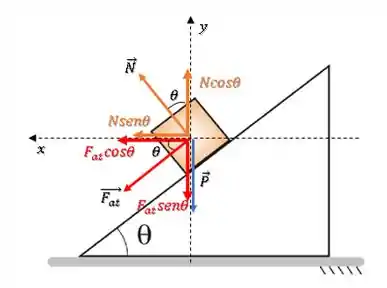
Agora, vamos fazer o somatório de forças em cada eixo. No eixo , já que o carro não tem aceleração vertical, temos um equilíbrio de forças:
Já no eixo , temos que o somatório das forças vai atuar como força centrípeta. Então:
A força centrípeta tem a seguinte expressão:
Onde, é a velocidade e é o raio. Então:
Ficamos então com essas duas equações:
Passo 3
A força de atrito estático é dada por:
Então, substituindo nas nossas equações:
Podemos colocar em evidência do lado esquerdo da equação e substituir por :
Vamos dividir uma equação pela outra:
Logo:
Passo 4
Para terminar, vamos entrar com as informações do nosso problema:
Devemos passar a velocidade de para :
Substituindo os valores, e usando ficamos com:
Resposta
(c)