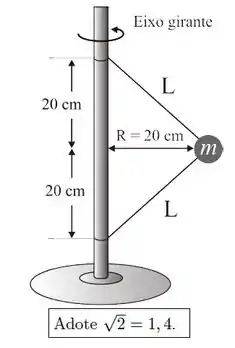
Uma partícula de massa está presa a uma haste vertical por duas cordas inextensíveis de massas desprezíveis. Quando colocada em movimento, a massa descreve um círculo horizontal de raio , com as cordas esticadas. A máxima tensão que cada fio pode suportar sem arrebentar é . Quando o sistema é colocado para girar em torno da haste com velocidade s podemos afirmar que:
Passo 1
Bom, ele tá querendo informação sobre a tração nos fios. Então vamos fazer um diagrama de forças e aplicar a segunda lei de Newton. Depois vamos comparar com esse valor máximo da tração, com isso veremos se um dos fios, ou ambos arrebentam.
Passo 2
Vamos começar com o diagrama de forças
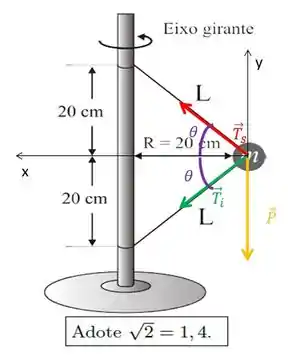
Vamos aplicar a segunda lei em x e em y:
Em x, temos:
Onde que é a aceleração centrípeta. Podemo usar que e ficamos com:
Decompondo as trações superior e inferior usando o eixo de coordenadas da figura, teremos:
Onde é o ângulo da figura. E o cosseno vale:. Já passei o comprimento do fio para metros. Usando o teorema de Pitágoras no triangulo retângulo, temos que
Então:
substituindo os valores,(NO SI!!) temos:
Show!! Isso foi o que conseguimos fazendo a segunda lei na direção x. Agora vamos fazer a mesma coisa, mas na direção y.
Passo 3
Em y, a força resultante é zero, pois não há movimento. Então:
O vale:
Então:
Substituindo os valores:
Notem que temos um sistema de 2 equações:
Resolvendo isso, temos:
e
Como o enunciado disse que a tração máxima que o fio aguenta sem arrebentar é 1,5N, temos que o fio superior arrebenta, já que a tração nele é maior que o valor máximo.
Resposta
O fio superior arrebenta.