Sobre o tampo de uma mesa horizontal sem atrito, dois blocos (massas m e M, onde M>m) executam um movimento circular com velocidade escalar constante ) ao redor do ponto O, onde uma corda de comprimento L, esticada na horizontal, prende o bloco M. Como há atrito entre os blocos, seus centros se mantêm alinhados e o bloco m não desliza sobre o bloco M. Use g como aceleração da gravidade.

- Faça o diagrama de forças sobre cada bloco
- Determine o módulo de todas as forças normais sobre cada bloco em função de m, M e g.
- Encontre uma expressão para o coeficiente de atrito μ entre os blocos em termos de v, L e g. Qual é o tipo de atrito envolvido: estático ou cinético? Justifique.
- Determine uma expressão para o módulo da tensão T na corda em termos de m, M, v e L. O valor de T é maior, menor ou igual ao módulo da força de atrito fat entre os blocos? Justifique.
Passo 1
- Segura aí!
Bloquinho:
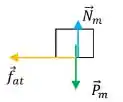
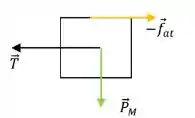
Blocão:
Passo 2
Na letra b devemos encontrar a força Normal em cada um dos blocos. No bloco de cima, o de massa m, temos apenas a força Peso contrária a Normal, então:
Já para o bloco de massa M, temos a Normal com a mesa e com o outro bloco! Então, temos:
Passo 3
c) Como sabemos, a força de atrito (fat) é dada por . Contudo, na situação descrita no problema acima, os blocos estão realizando um movimento circular de raio L em torno do ponto O, então também temos uma força centrípeta apontando naquela direção! Pelo bloco m, vemos que . Então, temos:
E o atrito entre os blocos é estático, já que o bloco m não se move em relação ao bloco M!
Pegô? :DDDD
Passo 4
d) Como queremos agora a Tensão, vamos olhar para o blodo de massa M. Daí, podemos tirar que:
Substituindo o valor da constante de atrito que encontramos na letra c, temos:Logo, isolando o T, temos:
Como , T é maior que fat, porque temos a massa M envolvida!
Resposta
a)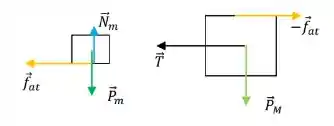
b) ;
c) ; estático
d) ; T > fat