Suponha que o coeficiente de atrito estático entre os pneus de um carro de massa m e a estrada onde ele trafega é
3) caso a pista seja inclinada na curva (curva compensada) e faça um ângulo com a horizontal, qual seria a maior velocidade escalar com que o carro completaria uma curva de raio R (ainda com atrito) sem deslizar?
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Nessa situação temos um carro que está fazendo uma curva em uma pista que não é horizontal, mas faz um ângulo com a horizontal.
Como nessa situação aqui:
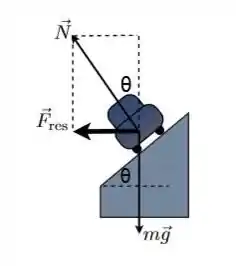
Como ele está fazendo uma curva, temos a força centrípeta como resultante das forças na direção horizontal
Já na vertical temos o peso (sempre vertical para baixo) e a normal (perpendicular à pista)
Ainda temos a força de atrito com a pista, que precisa ser adicionada ao desenho!
A ideia aqui é relacionar as forças existentes e identificar em qual situação a velocidade é máxima, como o problema pede! Precisamos lembrar que a força centrípeta está relacionada com a velocidade linear do carro! Então balancear as forças vai nos fornecerá uma equação para velocidade. Beleza? Vamos começar?

Passo 2
No item (1) dessa prova, calculamos a velocidade do carro para que ele não derrape na pista plana:
E é em relação a essa velocidade que vamos encontrar a velocidade máxima que o carro pode ter nessa pista ser derrapar

Outra coisa, a força de atrito pode atuar impedindo que o carro caia para baixo na pista, quanto impedindo que ele vá para fora. Mas qual situação ele terá a maior velocidade?
Vamos pensar o seguinte: aumentando a velocidade linear do carro, o carro tende a sair da pista, então para manter esse carro na pista, a força de atrito deve empurrá-lo para dentro da pista (no mesmo sentido que a força resultante)
O resultado disso é esse diagrama de forças:
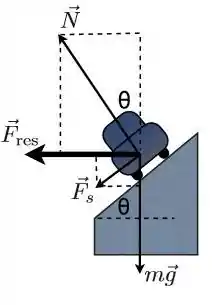
Beleza até aqui?
Com base nesse diagrama, podemos ver que tanto a força normal quanto a força de atrito podem ser decompostas, se assumirmos que ao longo da direção do peso passe um eixo vertical e ao longo da força resultante passe um eixo horizontal:
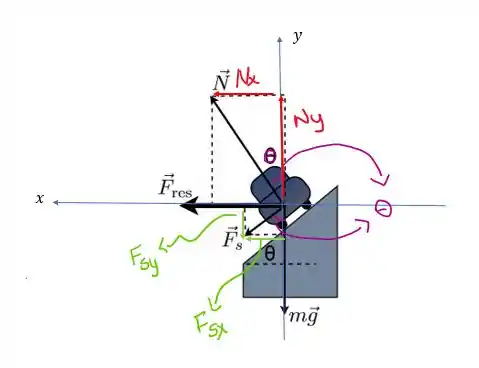
Nossa missão agora é equacionar as forças nas direções e ! Bora lá?
Na vertical a resultante é zero, já que o carro não ‘sai voando’ kkk
Como podemos ver ali em cima no diagrama e , aí a equação para direção vertical fica assim:
Podemos isolar o módulo da força normal :
Tranquilo?
Na horizontal temos que as componentes do atrito e da normal estão no mesmo sentido, e a soma delas é a resultante!
E pelo diagrama e , então a equação para a força resultante (que é a nossa força centrípeta) fica assim
E daqui podemos isolar a velocidade:
Beleza?
Passo 3
Mas e agora? Bom, temos duas equações e duas incógnitas: e
O problema nos pede o valor da velocidade, então vamos substituir a equação na equação , belezinha?
A equação (1) é:
Substituindo em (2):
Podemos cortar as massas em cima e embaixo:
E por fim, tirar a raiz quadrada dos dois lados:
E está aí! Essa é a velocidade máxima que o carro pode ter sem deslizar! A expressão da velocidade é dada em termos das quantidades conhecidas e .
E é isso!
Espero ter ajudado!