Os blocos A, B e C possuem mesma massa e repousam em uma superfície horizontal sem atrito. Os três são puxados por uma força horizontal de mesmo módulo e estão presos à uma parede vertical por um fio ideal conforme mostra a figura a seguir.
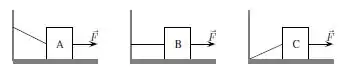
Considerando o módulo das forças normais exercida pelas superfícies sobre os blocos é correto afirmar que:
(a)
b)
(c)
(d)
(e)
(f)
(g)
Passo 1
Sabemos que os três blocos estão sendo puxados por uma mesma força e os três blocos estão presos, ou seja, estão em repouso.
Se eles estão em repouso, isso significa que a Força Resultante sobre eles é zero. Então, se queremos achar uma relação para as forças normais atuando sobre cada um dos blocos, podemos partir da Segunda Lei de Newton e considerar que o bloco está em equilíbrio.
Passo 2
Vamos analisar as forças sobre cada um dos blocos.
Bloco A:
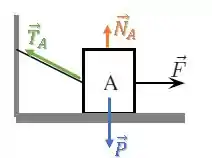
Bloco B:
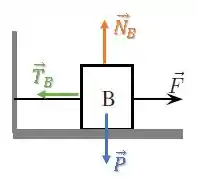
Bloco C:
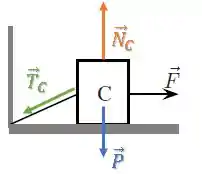
Qual a diferença entre as forças normais ?
A diferença vai ser devido à inclinação do fio, pois nos casos onde ele não está na horizontal, a força de Tração terá tanto uma componente na horizontal quanto na vertical.
Essa componente na vertical da força de Tração (em A e em C) vai influenciar na força normal sobre o bloco (equilíbrio vertical).
Passo 3
Vamos começar com o bloco B, pois as forças já estão na horizontal e vertical.
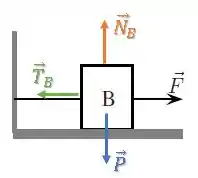
Vamos dar uma olhada na vertical, para relacionar :
No bloco A, vamos decompor a força de Tração e fazer o equilíbrio na vertical:
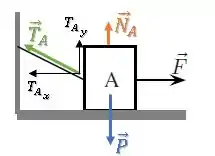
Como a componente da tração está para cima, ela ajuda a equilibrar a força peso, dando uma aliviada na força normal .
Já podemos ver que a força normal é menor que , pois é menor que a força peso .
No bloco C, vamos fazer a mesma coisa que no bloco A:
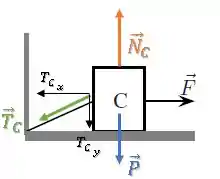
Agora, a coisa funciona ao contrário.
Existe uma componente da força de tração para baixo, então a força normal agora tem que equilibrar tanto quanto essa componente da tração.
Podemos ver que o módulo é maior que a força peso , assim, será maior que e :
Resposta
Letra (b)