Na figura abaixo, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas , , . Quando o conjunto é liberado a partir do repouso, (a) qual é a tensão da corda que liga a e (b) que distância percorre nos primeiros (supondo que não atinja a polia)?

Passo 1
Oi pessoal, tudo bem? Essa é uma típica questão e bloquinhos! Então vamos fazer passo a passo porque elas aparecem muito nas provas!
Esse é um problema que envolve a segunda lei de Newton e a cinemática. Primeiro, vamos lembrar que a segunda lei de Newton diz:
Podendo ser expandida para aplicação nas componentes, eixo por eixo.
Além disso, nessa questão usaremos a função horária da posição, tendo em vista que as caixas estão em MRUV:

A questão nos dá as massas das três caixas (, e ), nos diz que a velocidade inicial do conjunto é nula e nos pede a tensão na corda que liga e , além de pedir a distância percorrida pelo bloco nos primeiros .
Então a ideia é calcular a aceleração do sistema para depois calcular a tensão e a distância percorrida.
Mas relaxa, vou fazer passo a passo com você! Vamos começar?

Passo 2
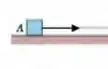
Lembrando que a mesa não oferece resistência ao movimento, a expressão que dá a tensão T na corda é:
Beleza?
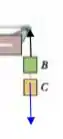 Agora vamos olhar para os blocos B e C:
Agora vamos olhar para os blocos B e C:
Podemos escrever a componente da segunda lei de Newton para o conjunto de caixa :
Tranquilo até aqui?
O que será que essas tensões tem em comum?? Elas são iguais! Isso proque é o mesmo fio! Apenas com a orientação diferente (por causa da polia)! Então se juntarmos essas duas equações fazendo podemos achar a aceleração!

Passo 3
Com essas duas equações em mãos, podemos substituir na equação para , pois os módulos das trações e são iguais e o módulo das acelerações são iguais também, tendo em vista que a polia é ideal e as caixas se movem juntas.

Do passo anterior:
Mas e , temos o seguinte:
Isolando :
Substituindo os valores conhecidos:
Beleza?

Passo 4
Letra (a): Com a aceleração do sistema calculada, podemos escrever a segunda lei de Newton apenas para o bloco :
Substituindo os valores conhecidos:
Isolando :
Show de bola!
Agora vamos para a letra (b)?

Passo 5
Letra (b): Para determinarmos a distância percorrida pelo bloco durante os iniciais, podemos usar a função horária da posição:
Considerando a origem do nosso sistema de coordenadas como sendo o ponto de partida e sabendo que ele parte do repouso, então:
Substituindo agora o valor da aceleração, que foi calculado anteriormente, e o tempo pedido:
E é isso galera! Espero ter ajudado!
Resposta
- ;
- .