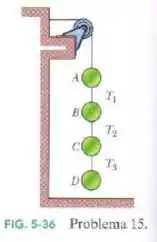
A Fig. 5-36 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco A, (b) do disco B, (c) do disco C e (d) do disco D?
Passo 1
Temos aqui um sistema em repouso, portanto, a aceleração de qualquer corpo que pegarmos para analizar será nula.
Vamos pensar juntos: Se pegarmos qualquer um dos discos para analisar, ou seja, fazer o diagrama de corpo livre, teremos duas trações agindo nele, além da força peso. Exceto no disco D, onde temos somente uma tração. Como todas as trações estão definidas no enunciado, a única incógnita fica sendo a massa de cada disco.
Passo 2
Vamos então fazer o diagrama de corpo livre de cada disco:
No disco A:
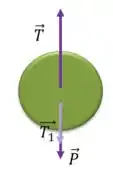
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de e de , portanto, usando :
Passo 3
- No disco B:
- No disco C:
- Do disco D:
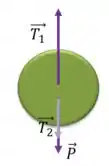
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de e de , portanto, usando :
Passo 4
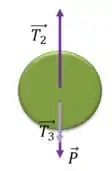
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de e de , portanto, usando :
Passo 5
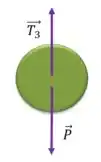
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de , portanto, usando :
- ''