USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 37a
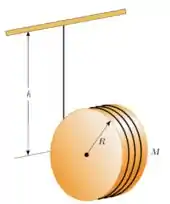
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.
(a) Qual é a tensão no fio?
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos um cilindro de raio e massa que é enrolado por um fio e solto para cair devido a ação da gravidade sendo a outra extremidade do fio presa em um lugar fixo.
Com isso queremos descobrir qual é a tensão no fio quando o cilindro começar a se desenrolar.
Tem ideia do que fazer? 👀
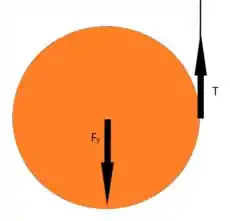
Se aplicarmos a segunda lei de Newton para esse caso, vamos obter as forças que atuam no cilindro é a força gravitacional, a força tração do fio e a força devido a aceleração do centro de massa do cilindro.
Ou seja, a força do centro de massa é igual a força gravitacional menos a forda tração .
Tranquilo até aqui?
Passo 2
Escrevendo a equação da força resultante, vamos obter
Isolando , vamos obter
Podemos relacionar o torque com a aceleração a partir da equação
Onde é igual a aceleração tangencial, ou seja
Isolando em e substituindo em
O momento de inercia de um cilindro é dado por
Substituindo em
Antes de substituir em , vamos reescrever (como o produto entre o raio e a força tangencial
No caso, a força tangencial é dada pela tração
Bacana, não é? 👀
Passo 3
Substituindo em , temos
Substituindo em
Isolando e simplificando...
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
