(Cap 4 – Ex 52) Para o sistema das Figuras 4-41a, 4-41b e 4-41c, encontre as massas e as tensões desconhecidas.

Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?

Quando estudamos as Leis de Newton precisamos sempre nos lembrar que estaremos falando sobre Forças. E quando recebemos um exercício que nos propõe um Diagrama de Corpo Livre, como no caso dos 3 itens, precisamos ter a mente bem aberta para visualizarmos com clareza quais são as possíveis forças que estarão presentes no sistema.

Para ajudar a entendermos as forças atuantes nos nossos Diagramas de Corpo Livre, usaremos as seguintes imagens:

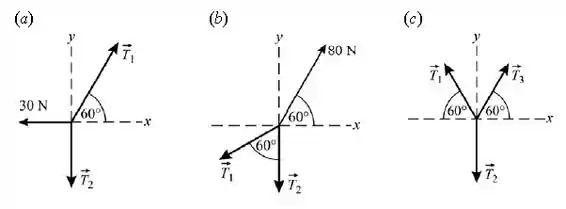
Perceba que foram inseridas linhas tracejadas representando os eixos e . Por que elas são necessárias? As forças são divididas em componentes de força. Mas como assim? No caso das Tensões aplicadas em um ângulo inclinado, por exemplo, não podemos dizer que essa determinada tensão exerce força na vertical OU na horizontal e sim devemos dizer que exerce força na vertical E na horizontal, ou seja, uma parcela da tensão é depositada para o componente e uma parcela no componente . E se a tensão estiver sobre um eixo? Isso significa que a componente desse eixo será igual a própria tensão e a componente no eixo oposto será zero.

Beleza, entendi toda essa teoria, mas onde isso irá me ajudar?

Por definição, temos que:

A somatória de forças (tensões) sobre o eixo é igual ao produto entre a massa e a aceleração gravitacional no eixo . O mesmo vale para o eixo . A somatória das tensões sobre é igual ao produto entre a massa e a aceleração gravitacional no eixo .

Para concluir, para que os sistemas se encontrem em repouso, e devem ser iguais a zero. Caso não fosse zero, então o sistema estaria em movimento.

Para o item (a), temos:

Resolvendo, temos que:

Como é o peso do objeto, podemos encontrar sua massa. Temos que: