Na figura ao lado, uma barra horizontal fina AB, de massa desprezível e comprimento , é presa a uma dobradiça em uma parede vertical no ponto A e sustentada em B por um fio ideal fino BC. O fio faz um ângulo com a horizontal. Um bloco de peso P pode ser movido para qualquer posição ao longo da barra, sendo a sua posição definida pela distância desde a parede até o seu centro de massa (veja a figura).
Sabe-se que a aceleração da gravidade no local é constante e aponta para baixo, agindo na direção paralela à parede vertical. Para tal situação, calcule:
- A tensão no fio. Expresse sua resposta em termos de , , e .
- A componente horizontal da força exercida sobre a barra pelo pino da dobradiça em . Expresse sua resposta em termos de , , e .
- A componente vertical da força exercida sobre a barra pelo pino da dobradiça em . Expresse sua resposta em termos de , e .
Passo 1
POW! Antes de começarmos o problema, o que acha de desenharmos sobre o sistema o diagrama de forças que está atuando nele?
Bem, basicamente temos 3 forças atuando no problema: a tração na corda (), a força peso do bloco , e uma força no pino que o mantém preso pra cima...
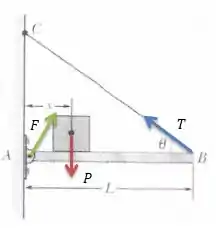
Repare que o problema está em equilíbrio, então o somatório das forças tem que ser igual a ...
E o torque total também tem que ser igual a ...
Passo 2
Na letra queremos justamente encontrar a tração na corda em termos de , , e . Uma forma de fazer isso é usando o fato de que o sistema está em equilíbrio, logo...
Escolhendo a dobradiça como referência, vamos calcular o torque total de cada força em relação à dobradiça.
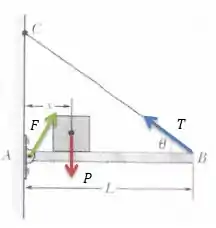
Repare que as únicas forças que fazem torque em relação a dobradiça é a peso e a tração , afinal a força está em cima da dobradiça e portanto ele não faz nenhum torque na barra. O torque da força peso é...
O é porque o peso tende a girar a barra no sentido horário. Já o torque da força de tração é...
O é só para pegar a componente vertical da força de tração...
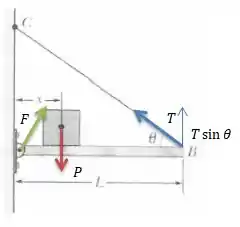
O torque total então será...
Logo...
Logo, o torque em função dos carinhas pedidos no problema será...
Passo 3
A componente horizontal da força que está atuando na barra é ...
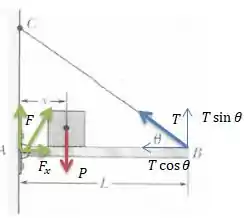
Pelo fato de o sistema estar em equilíbrio, sabemos que as componentes horizontais de todas as forças devem se somar . Como só temos como componente horizontais a (força que queremos encontrar) e também a ...
O fato de estar negativo é porque essa componente está contrária a força ...
Como encontramos no passo anterior...
Passo 4
Nesse caso, queremos encontrar a componente vertical da força que atua na dobradiça. Então, de modo análogo, a soma das forças verticais tem que ser iguais a ...
Resposta
Letra A:
Letra B:
Letra C: