A3 T3 T2
Assinale abaixo a área do paralelogramo definido pelos vetores e em :
Passo 1
Essa é complicada. Se liga, se a gente tem um paralelogramo qualquer:
Deixando ele retinho pra facilitar as contas ficamos com:
E sua área é dada pela base vezes a altura, ou seja:
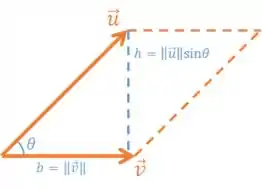
Vamos fazer aparecer uma raiz nesse negócio já que nas opções só tem raiz:
Agora a gente vai reescrever o seno como :
Agora a gente substitui uma das definições de produto interno, que é:
E chegamos na nossa resposta, letra ! Como eles esperavam que alguém fosse pensar nisso na prova eu realmente não sei, mas né . . .
Resposta
Letra
Exercícios de Livros Relacionados
Considere R 2 ,R 3 e R 4 com o produto interno euclidiano. Em cada parte, encontre o cosseno do ângulo entre u e v . u = 1 , - 3 , v = 2,4 u = - 1,0 , v = 3,8 u = - 1,5 , 2 , v = 2,4 , - 9 u = 4,1 , 8
13. Quais as condições devem satisfazer a e b para que a matriz a + b b - a a - b b + a seja ortogonal?
Dizemos que um operador matricial R 2 é rígido se mantiver o comprimento dos vetores, e preserva ângulo se não mudar o ângulo entre vetores não nulos.(a) Dê o nome de dois tipos distindos de operadore
O resultado do Exercício 15 tem um análogo para matrizes ortogonais 3 × 3 , como segue. Pode ser provado que a multiplicação ortogonal A de tamanho 3 × 3 é uma rotação em torno de algum eixo se d e t
7. Repita o Exercício 6 com theta = (pi)/(3) .